zivЕсли

положительно определено, то

тоже положительно определено. Это Вы верно заметили. Однако, положительная определенность для

нам вовсе не дана. С другой стороны, и доказать ее тоже не требовалась. Т.е. Вы не совсем то доказали, даже в одну сторону. Тем не менее, поскольку Вы прилагали усилия, то вот Вам решение.
То, что

положительно определена, Вы, по существу, уже доказали. Также легко видеть, что

в точности тогда, когда
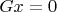
.
Предложение. Пусть  --- действительное векторное пространство,
--- действительное векторное пространство,  и
и  --- квадратичные формы на
--- квадратичные формы на  , причем
, причем  неотрицательно определена. Пусть
неотрицательно определена. Пусть  --- ядро формы
--- ядро формы  . Тогда эквивалентны два условия:
. Тогда эквивалентны два условия:
(1) форма  положительно определена для некоторого
положительно определена для некоторого
(а тогда и для любого достаточно большого)  ;
;
(2) ограничение формы  на
на  положительно определено.
положительно определено.
Доказательство. (1)

(2). Возьмем

такое, что

положительно определена. Если

--- любой вектор из

, то

. Но

, значит

. Это и означает, что

положительно определена.
(Замечание. Это и есть легкая часть утверждения. Я думал, именно это Вы и умеете доказывать "в одну сторону".)
(2)

(1). Это сложнее. Здесь надо использовать соображения компактности. Не знаю, какая у Вас подготовка, поэтому напишу поэлементарнее.
Выберем и зафиксируем на пространстве

какую-нибудь положительно определенную квадратичную форму

. Например, можно считать, что

--- пространство вектор-столбцов, а

--- обычный евклидов квадрат (сумма квадратов координат). Пусть

--- единичная сфера относительно

. Для любого

существует
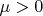
такое, что

.
Будем рассуждать от противного. Предположим, что

не является положительно определенной ни для какого

. Для каждого натурального числа

возьмем

такое, что

. Можно даже считать, что

, для всех

.
Поскольку множество

ограничено, то последовательность

содержит сходящуюся подпоследовательность. Ограничиваясь этой подпоследовательностью, видим, что мы установили следующее:
существуют возрастающая последовательность положительных чисел  и последовательность точек
и последовательность точек  такие, что
такие, что  , для всех
, для всех  ; последовательность
; последовательность  сходится; а последовательность
сходится; а последовательность  стремится к
стремится к  .
. Пусть

--- предел. Мы утверждаем, что

,

(т.е.

), и

. (Отсюда получится противоречие).
Поскольку

, а

--- непрерывная функция на

, то и

, значит

.
Так как

неотрицательно определено, то из

следует

. Переходя к пределу, получаем

.
Последовательность

ограничена, значит существует

такое, что

. Отсюда

,

. Переходя в этом соотношении к пределу, получаем

. Но

неотрицательно определено, значит на самом деле

.
