Обработка результатов измерений. Оценка станд. отклонения.

[antonio.troitsky]

Доброго времени суток.

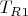
Имеются результаты измерений интенсивности сигнала от времени. В данном случае рассматривается 2 момента времени $T_R_1$ и $T_R_2$. Для каждого $T_R$ получается $n$ интенсивности сигнала ($S_1$ и $S_2$). Имеется искомая величина $T$, которая выражается через эти 2, т.е. $T=T(S_1, S_2)$.

Вопрос касается оценки стандартного отклонения косвенного измерения величины $T$ или $\sigma_T$.


Находим средние значения и стандартные отклонения интенсивностей сигналов $\bar{S_1}$ и $\bar{S_2}$, $\sigma_S_1$ и $\sigma_S_2$.
Если записать формулу оценки стандартного отклонения для физической величины $T$ при косвенном измерении $\sigma_T(1) = \sqrt{(\frac{\partial T}{\partial S_1} \sigma_S_1)^2 + (\frac{\partial T}{\partial S_2} \sigma_S_2)^2}$, то нам надо подставить значения стандартного отклонения $\sigma_S_1$ и $\sigma_S_2$.
Можно получить оценку значения величины $T$ как $T = T(\bar{S_1}, \bar{S_2})$.

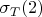
Допустим на тех же самых $n$ измерениях мы получаем $n$ значений величин $T$. Находим оценку среднего значения $\bar{T}$ и стандартного отклонения $\sigma_T(2) $ уже из $n$ значений величин $T$.

Вопрос.

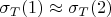
Должны ли "примерно" совпадать значения $\sigma_T(1) \approx\sigma_T(2) $ ?

[LMA]

antonio.troitsky в сообщении #1401816 писал(а):

Должны ли "примерно" совпадать значения $\sigma_T(1) \approx\sigma_T(2) $ ?

Никаких ограничений я не заметил. Поэтому ответ --- нет.

[antonio.troitsky]

LMA в сообщении #1401897 писал(а):

antonio.troitsky в сообщении #1401816 писал(а):

Должны ли "примерно" совпадать значения $\sigma_T(1) \approx\sigma_T(2) $ ?

Тогда зачем вообще оценивать случайную погрешность первым способом? Если можно просто оценить стандартное отклонение искомой величины?

[LMA]

Я в обозначениях запутался.
Они будут примерно совпадать, если дисперсии достаточно малы (когда можно ограничиться линейными членами разложения величины $T$ в ряд Тейлора).

[antonio.troitsky]

LMA в сообщении #1401980 писал(а):

Я в обозначениях запутался.
Они будут примерно совпадать, если дисперсии достаточно малы (когда можно ограничиться линейными членами разложения величины $T$ в ряд Тейлора).

Вот тут как раз и проблема в том, что у меня они отличаются достаточно прилично.