Добрый день, помогите разобраться с определением.
***
Цитата:

,
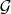
—

-алгебры подмножеств

и

соотв.;

называется

-измеримой, если

Что подразумевают, когда говорят?:
Цитата:

— измерима относительно

Значит, что есть некая

, что

—

-измерима? Из контекста (
https://ru.wikipedia.org/wiki/Условное_математическое_ожидание#УМО_относительно_σ-алгебры) мне не удалось понять этого