Здравствуйте, уважаемые пользователи форума. Есть одна задачка, но сам я затрудняюсь в решении, надеюсь, вам она будет интересна.
Имеется ломаная (незамкнутая), состоящая из трёх отрезков. Даны координаты на плоскости начала и конца ломаной и длины этих отрезков. Нужно найти координаты двух промежуточных изломов, если известно что угол между первым и вторым отрезком соотносится с углом между вторым и третьим как некоторая величина (тоже дана).Можно попробовать её переформулировать так: в произвольном четырёхугольнике известны длины двух сторон, обоих диагоналей и соотношение двух противолежащих углов, построить этот четырёхугольник.
Если представить себе неподвижными начало и конец ломаной, то промежуточные точки должны находиться на окружностях с таковыми центрами радиусами в длину отрезков. Обозначим точки как A, B, C, D. Тогда можно составить систему из 4-х уравнений:




,
где x и y - координаты соответствующих точек, |XX| - длина отрезка, c - соотношение углов.
Примерно так:
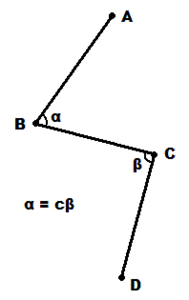
Можно, допустим, для простоты положить точку B в начало координат, а C - справа на ось Ox. Тогда уравнения можно собрать в кучу примерно так:


,
где d - расстояние между A и D.
Дальше уже с трудом представляю, что с этим делать и как решать.