Так же в порядке эксперимента было сделано следующее но по-моему это тупиковый вариант:
(Оффтоп)
Повернём систему координат так чтобы

и переформулируем уравнение (3) в терминах

:

, а так же получим

. Заменив

,

, получим в итоге такое уравнение:

. В нём нет явной тригонометрии, и в нём явно указаны компоненты

искомой кривой, но кажется это ничем не помогает его решить.
Само поведение

можно наглядно описать с помощью следующей картинки (нарисовано в системе координат где ось

параллельна

):
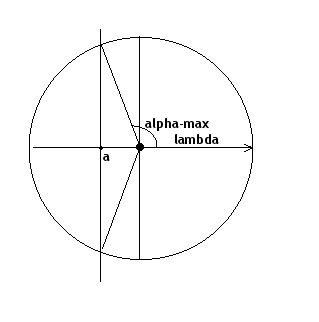
Угол

не может приводить к

. В самой точке

происходит разворот вращения вектора направления

- смена знака

. Если

то эта точка отсутствует.Если

то в этой точке будет

и

- то есть попасть в ней можно только из соответствующего начального условия, и кривая тогда будет строго прямой (это одно из решений, которое не следует забывать). Поведение

в целом напоминает поведение физического маятника, с вектором "гравитационного поля"

и полной энергией

. Возможно, оно даже в точности с ним совпадает, но в данном случае это незачем выяснять.
Введём

, тогда из уравнений (3), (4) и (5) можно вынести

за скобки, и теперь при увеличении/уменьшении

, при сохранении постоянным

, график

будет кратно сжиматься/растягиваться вдоль оси

, а искомая кривая - кратно сжиматься/растягиваться по обеим своим осям. Поэтому для упрощения дальнейших расчётов можно взять

, а затем уже готовые решения просто масштабировать в зависимости от этого параметра.
Теперь рассмотрим случай, который был заявлен в самом начале задачи - много фиксированных точек, через которые надо провести кривую. Очевидно, что каждый из сегментов этой кривой в отдельности будет решением своей задачи - он будет давать локальный минимум функционала при зафиксированных

,

,

,

. Если бы это было не так, то можно было бы, не трогая остальную кривую, заменить этот сегмент на более оптимальный, получив лучшую кривую в целом.
Если проварьировать полный интеграл по всей кривой, получим сумму значений, посчитанных по формуле (1) для каждого сегмента. Интегральные слагаемые нулевые, так как сегмент - решение более простой задачи выше, неинтегральные слагаемые с множителем

нулевые, так как в фиксированных точках

. Из оставшегося слагаемого сокращается всё, кроме двух раз, если учесть дифференцируемость кривой (

не меняет свой значение в точках сопряжения) и следующее из этого необходимое условие отсутствия ступенек

в этих же точках. Остаётся только
![$$\sum_k \frac {dS_k}{d\varepsilon} = \sum_k \left[ L_{\vec f''} \vec g' \right]_{T_k}^{T_{k+1}} = \left[ L_{\vec f''} \vec g' \right]_{0}^{T} = \left[ 2 \vec v' \vec g' \right]_{0}^{T}$$ $$\sum_k \frac {dS_k}{d\varepsilon} = \sum_k \left[ L_{\vec f''} \vec g' \right]_{T_k}^{T_{k+1}} = \left[ L_{\vec f''} \vec g' \right]_{0}^{T} = \left[ 2 \vec v' \vec g' \right]_{0}^{T}$$](https://dxdy-02.korotkov.co.uk/f/9/c/b/9cbd8d841eafad9a373a63c951c176ae82.png)
Из необходимого равенства нулю этой производной и необходимости выполнять это при любых

следует условие

- то есть на самых крайних точках не должно быть искривления, что, вобщем-то, и так было интуитивно понятно.
Из условия сопряжения

, оно же

- сохранение кривизны в промежуточных точках, следует (с учётом уравнения (3)), что в этих точках должно сохраняться

- проекция

на текущее направление кривой.
Осталось не очень понятным, как так вышло, что повороты направлений в промежуточных точках ни на что не влияют, но, вероятно, там не так просто их повернуть, не затронув что-то ещё. Думаю это станет яснее после расчёта кривых на сегментах.