Вычитание в аддитивной абелевой группе

[project15]

Имеем $A$ - аддитивную абелеву группу. Ее элементы будем называть числами.
Вычитание можно определить двумя способами.

1. Назовем разностью $a-b$ чисел $a$ и $b$ число $c\in A$, такое что $c = a + (-b)$. Существование и единственность $c$ очевидна, т.к. сумма определена и единственна для любой пары чисел из $A$.

2. Назовем разностью $a-b$ чисел $a$ и $b$ решение уравнения $x + b = a$, $x\in A$. Существование очевидно - можно взять $c = a + (-b)$. Непосредственной проверкой убедимся, что $c$ удовлетворяет определению разности. Как доказать единственность? Что такое уравнение в данном случае? (я склоняюсь к тому, что уравнение - это предикат, заданный на множестве $A$ - можно ли так понимать смысл слова "уравнение"?). То доказательство единственности $c$ которое я видел использует слова наподобие "прибавим к обеим
частям уравнения $(-b)$...". Почему к обеим частям уравнения можно прибавлять поровну и какое уравнение после этого получится (равносильное? почему?). Зачем вообще вводить новую сущность (уравнение), если можно обойтись без него, как в первом определении? Если определения равносильны, то я не понимаю, почему в литературе используют вариант с уравнением, когда можно просто сказать: разность $a$ и $b$ - это сумма $a$ и противоположного для $b$?

[svv]

project15 в сообщении #1389851 писал(а):

Как доказать единственность?

Пусть $c$ — разность $a$ и $b$ во втором смысле, то есть такое $c$, что $c+b=a$. Тогда
$c=c+0=c+(b+(-b))=...$
Дальше понятно?

[project15]

svv

Цитата:

Дальше понятно?

Нет. Можете написать продолжение?

[Munin]

project15 в сообщении #1389851 писал(а):

Имеем $A$ - аддитивную абелеву группу.

Надеюсь, вы в курсе, что слова "абелева группа" означают сущность, а слово "аддитивная" - способ записи этой сущности. Например, одну и ту же группу можно условиться записывать разными способами: аддитивным, мультипликативным, другими.

project15 в сообщении #1389851 писал(а):

Что такое уравнение в данном случае?

Здесь вполне можно понимать "уравнение" в наивном смысле. Некоторое равенство, которое должно становиться истинным при каких-то значениях неизвестных величин.

project15 в сообщении #1389851 писал(а):

я склоняюсь к тому, что уравнение - это предикат, заданный на множестве $A$ - можно ли так понимать смысл слова "уравнение"?

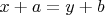
Да, если у вас одна неизвестная величина $x.$ Уравнения могут быть заданы и для нескольких неизвестных, например, $x+a=y+b$ - тогда это предикат на $A\times A=A^2.$ (Если используются операции из разных множеств, типа умножения вектора на скаляр, то соответственно будет декартово произведение соответствующих множеств.)

project15 в сообщении #1389851 писал(а):

То доказательство единственности $c$ которое я видел использует слова наподобие "прибавим к обеим частям уравнения $(-b)$...". Почему к обеим частям уравнения можно прибавлять поровну и какое уравнение после этого получится (равносильное? почему?).

Левая и правая части уравнения - это какие-то элементы группы, обозначим их $L$ и $R.$ Тогда из аксиом группы легко проверяется

$$L=R\quad\Longleftrightarrow\quad L+(-b)=R+(-b)$$

для произвольного $b\in A.$ Проверьте!

project15 в сообщении #1389851 писал(а):

Зачем вообще вводить новую сущность (уравнение), если можно обойтись без него, как в первом определении?

Затем, что вообще говоря, нас будет дальше интересовать, как решать разные уравнения. Хорошо, уравнение вида $x+a=b$ вы решили. А как насчёт уравнения $x+x=a$? Его вы всегда умеете решать? Всегда ли в группе есть хоть один ненулевой $a,$ для которого есть решение? Уже не такие простые вопросы. 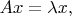Ну и всё это - подготовка для уравнений типа $x^3+1=0,$ $x^n+y^n=z^n,$ $Ax=\lambda x,$ $AX+XB=0,$ $e^X=A,$ $(d^2/dt^2+a^2)x=0,$ и многих других увлекательных уравнений. Так что вам здесь просто подчёркивают, что для одного уравнения некоторого типа - вопрос исчерпывающе решён.

[svv]

project15 в сообщении #1389862 писал(а):

Нет.

$...=(c+b)+(-b)=a+(-b)$
Мы для некоторой разности $c$ показали, что она равна $a+(-b)$. Мы можем то же проделать для другой разности $c'$. Вывод?

[Lia]

svv в сообщении #1389867 писал(а):

Вывод?

Все-таки надо было уносить тему в Карантин раньше.

[Lia]

Тема перемещена из форума «Помогите решить / разобраться (М)» в форум «Карантин»
по следующим причинам:

- отсутствуют собственные содержательные попытки решения задач(и).

Исправьте все Ваши ошибки и сообщите об этом в теме Сообщение в карантине исправлено.
Настоятельно рекомендуется ознакомиться с темами Что такое карантин и что нужно делать, чтобы там оказаться и Правила научного форума.