Всем привет. Речь о возможной опечатке в книге. А может не вижу ошибку у себя. Большая просьба помочь увидеть:)
Рассматривается схема Бернулли, выражаемая тройкой

, где

- пространство элементарных событий; вероятность элементарного события определяется выражением

Пусть на

задана случайная величина

В книге Ширяева "Вероятность" (1980) утверждается, что математическое ожидание

а у меня получается

. Считал следующим образом

где


только когда все
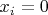
. Поэтому

, и значит

где

Если это верно, то
