e^n иррационально

[икс и грек]

Пусть $n$ - натуральное число. Как доказать, что $e^n$ - иррационально?

[Brukvalub]

Рассуждением с рядом, в который разлагается экспонента, аналогично тому, как доказывается иррациональность самого е.

[bot]

Дык, $e$ транцендентно и следовательно не может удовлетворять уравнению типа $qx^n-p=0$
Или требуется обойтись без этого?

[T-Mac]

Пусть $e^n$ - рационально, тогда $e$ - рационально, а это не верно и значит , что $e^n$ - иррационально

[Бодигрим]

T-Mac писал(а):

Пусть $e^n$ - рационально, тогда $e$ - рационально, а это не верно и значит, что $e^n$ - иррационально

Пусть $(\sqrt2)^2$ - рационально, тогда $\sqrt2$ - рационально, а это не верно и значит, что $(\sqrt2)^2$ - иррационально

[T-Mac]

Да действительно, ступил.

[Профессор Снэйп]

икс и грек писал(а):

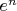
Пусть $n$ - натуральное число. Как доказать, что $e^n$ - иррационально?

Ха! Как ни странно, я помню, как этот факт доказывался у нас в курсе матана, поскольку совсем недавно писал телегу на близкую тему. Поскольку время позднее и на вечер никаких серьёзных дел не запланировано, напишу это доказательство подробно.

Зафиксируем положительные целые числа $p, q$ и пусть $r=p/q$. Мы докажем, что число $e^r$ иррационально.

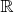
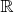
Если $f$ --- функция из $\mathbb{R}$ в $\mathbb{R}$, дифференцируемая бесконечное число раз, то для целого положительного $i$ через $D^i f$ будем обозначать $i$-ую производную этой функции. Для $i=0$ считаем, что $D^0 f = f$. Мы считаем, что натуральный ряд начинается с нуля.

Лемма 1. Если $f(x)$ --- многочлен степени $n \in \mathbb{N}$ с действительными коэффициентами, то

$$ \int f(x)e^x dx = \left( \sum_{i=0}^n (-1)^i D^i f(x) \right) e^x + C $$

Доказательство.

$$ \frac{d}{dx} \left( \sum_{i=0}^n (-1)^i D^i f(x) \right) e^x = \left( \sum_{i=0}^n (-1)^i D^{i+1} f(x) \right) e^x + \left( \sum_{i=0}^n (-1)^i D^i f(x) \right) e^x = $$

$$ = D^0 f(x) e^x + (-1)^n D^{n+1} f(x) e^x = f(x)e^x \,\,\qed $$

Пусть теперь для каждого натурального $n$

$$ \Psi_n(x) = \frac{x^n(p-qx)^n}{n!} \,\,\, (1) $$

По формуле бинома Ньютона имеем

$$ \Psi_n(x) = \sum_{i=0}^n \frac{(-1)^ip^{n-i}q^ix^{n+i}}{i!(n-i)!} \,\,\, (2) $$

Лемма 2. Для любых натуральных $n$ и $i$ числа $D^i \Psi_n(0)$ и $D^i \Psi_n(r)$ --- целые.

Доказательство. При $i<n$ имеем $D^i \Psi_n(0) = D^i \Psi_n(r) = 0$, так как $0$ и $r$ --- корни многочлена $\Psi_n(x)$ кратности $n$. При $i>2n$ справедливы те же самые равенства, поскольку степень многочлена $\Psi_n(x)$ равна $2n$.

Пусть теперь $n \leqslant i \leqslant 2n$. Тогда $i=n+k$ для некоторого целого $k \in [0,n]$. Из формулы (2) получаем

$$ D^i \Psi_n(x) = \sum_{j=k}^n \frac{(-1)^jp^{n-j}q^j(n+j)!}{j!(n-j)!(j-k)!}x^{j-k} = k! \sum_{j=k}^n (-1)^j C_j^k C_n^j C_{n+j}^j p^{n-j} q^j x^{j-k} $$

Подставляя в это равенство нужные нам значения, имеем

$$ D^i \Psi_n(0) = (-1)^k k! C_n^k C_{n+k}^k p^{n-k} q^k \in \mathbb{Z} $$

и

$$ D^i \Psi_n(r) = k! p^{n-k} q^k \sum_{j=k}^n (-1)^j C_j^k C_n^j C_{n+j}^j \in \mathbb{Z} \,\,\, \qed $$

Пусть теперь

$$ I_n = \int_0^r \Psi_n(x) e^x dx $$

По лемме 1 из формулы Ньютона-Лейбница получаем

$$ I_n = \left( \sum_{i=0}^{2n} (-1)^i D^i \Psi_n(r) \right) e^r - \sum_{i=0}^{2n} (-1)^i D^i \Psi_n(0) $$

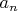
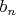
Из этого равенства и леммы 2 заключаем, что для каждого $n \in \mathbb{N}$ существуют целые числа $a_n$ и $b_n$, такие что

$$ I_n = a_n e^r + b_n \,\,\, (3) $$

Заметим теперь, что для каждого $n \in \mathbb{N}$ справедливо $I_n > 0$ и

$$ \lim_{n \to \infty} I_n = 0 $$

Первое следует из того, что интегрируемая функция положительна на всём промежутке интегрирования. Второе легко выводится из следующих двух фактов:

1) $\Psi_n(x) \leqslant (r^np^n)/n!$ для всех $x \in [0,r]$;

2) $I_n \leqslant (r^{n-1}p^n)/n!$.

Предположим, наконец, что число $e^r$ рационально. Тогда для некоторых $u,v \in \mathbb{Z}$, таких что $v > 0$, справедливо равенство $e^r = u/v$. Отсюда и из формулы (3) выводим, что

$$ v I_n = a_n u + b_n v $$

Однако величина в левой части равенства положительна при любом $n$ и стремится к $0$ при $n \to \infty$, а величина в правой части равенства для любого $n$ является целым числом. Полученное противоречие завершает доказательство.

[RIP]

Brukvalub писал(а):

Рассуждением с рядом, в который разлагается экспонента, аналогично тому, как доказывается иррациональность самого е.

Brukvalub
А Вы сами пробовали это проделывать?

На самом деле тем методом, который описал Профессор Снэйп (кстати, Лемма 1 называется тождеством Эрмита) легко доказать и трансцендентность $e$ (можно и чуть попроще). А вот иррациональность $e^n$ при натуральном $n$ можно доказать гораздо проще, но я к сожалению не помню как.

[Профессор Снэйп]

RIP писал(а):

На самом деле тем методом, который описал Профессор Снэйп (кстати, Лемма 1 называется тождеством Эрмита) легко доказать и трансцендентность $e$ (можно и чуть попроще).

А что тут можно упростить? И, кстати, как приспособить всё это к доказательству трансцендентности? Хотя последнее вроде понятно: нужно вместо $\Psi_n(x) e^x$ рассматривать что-то вроде $\Psi_n(x) P(e^x)$ при $p=q=1$, где $P$ --- многочлен, для которого $P(e)=0$. Ну и получать противоречие. Или я ошибаюсь? Да, похоже что это действительно не лучшая идея.

А ещё мне кто-то говорил, что этот метод можно приспособить для доказательства иррациональности $\pi$. Дескать, вместо экспоненты рассматриваем синус и что-то там вроде получается... Но я не вижу, как это можно сделать.

[RIP]

Профессор Снэйп писал(а):

А ещё мне кто-то говорил, что этот метод можно приспособить для доказательства иррациональности $\pi$. Дескать, вместо экспоненты рассматриваем синус и что-то там вроде получается... Но я не вижу, как это можно сделать.

viewtopic.php?p=48516#48516

[Профессор Снэйп]

RIP писал(а):

http://dxdy.ru/post48516.html#p48516

Да, действительно не очень сложно. Спасибо за ссылку.

[Brukvalub]

RIP писал(а):

Brukvalub
А Вы сами пробовали это проделывать? Wink

Всех выкладок на бумажке я не проводил, просто вспомнил соответствующий фрагмент доказательства из Фихтенгольца, мысленно пробежался по нему, и мне показалось, что все пройдет и в этом случае.

[RIP]

Профессор Снэйп писал(а):

А что тут можно упростить?

Пусть $a\in\mathbb N$. Обозначим $I_n=\int_0^\infty\frac{x^{n-1}(x-a)^n}{(n-1)!}e^{-x}dx$, где $n$ - натуральное число. Очевидно, что $I_n$ - целое число, причём $I\equiv(-a)^n\pmod n$. Далее, $e^aI_n=A_n+\varepsilon_n$, где $A_n=e^a\int_a^\infty\frac{x^{n-1}(x-a)^n}{(n-1)!}e^{-x}dx=\int_0^\infty\frac{(x+a)^{n-1}x^n}{(n-1)!}e^{-x}dx$ - целое число, делящееся на $n$, а $\varepsilon_n=e^a\int_0^1\frac{x^{n-1}(x-a)^n}{(n-1)!}e^{-x}dx$ - "мелочь". Если $e^a=p/q$, то $pI_n-qA_n=q\varepsilon_n$ - целое число, не делящееся на $n$, и строго меньшее 1 по модулю для подходящих значений $n$. Мне это доказательство кажется проще.

Профессор Снэйп писал(а):

И, кстати, как приспособить всё это к доказательству трансцендентности?

Удобнее работать с тождеством

$$e^z\int_0^zf(x)e^{-x}dx=F(0)e^z-F(z),$$

где $f(x)$ - многочлен, $F(x)=\sum_{n\ge0}f^{(n)}(x)$.
Сам Эрмит в качестве $f(x)$ взял $\frac{\bigl(x(x-1)\ldots(x-m)\bigr)^n}{n!}$. В итоге большую часть статьи (10-15 страниц) у него занял подсчёт некоторого определителя. Стилтьес чуть-чуть "подправил" $f(x)$, в результате чего никаких определителей считать стало не нужно и док-во можно изложить на паре страничек.
Это я некий экскурс в историю привёл по своим записям спецкурса по трансцендентным числам (поэтому не могу гарантировать достоверность информации). Мне лень вдаваться в детали доказательств.

Добавлено спустя 25 минут 52 секунды:

Brukvalub писал(а):

Всех выкладок на бумажке я не проводил, просто вспомнил соответствующий фрагмент доказательства из Фихтенгольца, мысленно пробежался по нему, и мне показалось, что все пройдет и в этом случае.

Мне раньше тоже так казалось, пока я не попробовал.

[Профессор Снэйп]

RIP, спасибо за инфу.

По поводу рассуждений с рядом, в который разлагается экспонента. Меня интересует вот такой вопрос.

Пусть $n > 0$ --- натуральное. Тогда, очевидно, найдётся натуральное $k(n)$, такое что

$$ [e^n] = \left[ \sum_{i=0}^{k(n)} \frac{n^i}{i!} \right] $$

(квадратные скобки обозначают целую часть). Можно ли установить для $k(n)$ какую-нибудь хорошую оценку сверху?

Под "хорошей" я понимаю оценку, выраженную через степени, факториалы и другие достаточно медленно растущие функции. Скажем, $k(n) \leqslant n^{n^{n!}} + 10^{100}$ --- это для меня хорошая оценка. Если более точно, то хорошая оценка --- это оценка вида $k(n) \leqslant A(a,n,n) + C$, где $a, C \in \mathbb{N}$ --- некоторые фиксированные натуральные константы, а $A$ --- функция Аккермана (определение см. здесь).

[RIP]

Можно. Делается это, например, следующим образом. Сначала обобщим Вашу Лемму 1.
Лемма 1'. Пусть $f(z)$ - многочлен степени $M$, $F(z,x)=\sum_{k=0}^Mf^{(k)}(z)x^{M-k}$. Тогда

$$F(0,x)e^{zx}-F(z,x)=x^{M+1}e^{zx}\int_0^zf(\zeta)e^{-\zeta x}d\zeta.\qed$$

Пусть $N>0$ - целое число, которое мы выберем позжее. Положим

$$f_0(x)=\frac{x^N(n-x)^{N+1}}{N!},\ f_1(x)=\frac{x^{N+1}(n-x)^N}{N!},$$

$$F_r(z,x)=\sum_{k=0}^{2N+1}f_r^{(k)}(z)x^{2N+1-k}\ (r=0,1),$$

$$\Delta(x)=\left|\begin{matrix}F_0(0,x)&F_0(n,x)\\F_1(0,x)&F_1(n,x)\end{matrix}\right|.$$

Лемма 2. Если $x\ne0$, то $\Delta(x)\ne0$.
Док-во. Из определения $\Delta(x)$ очевидно, что это многочлен степени (в точности) $2N+2$. Умножим первый столбец $\Delta(x)$ на $e^{nx}$ и вычтем из второго. Из Леммы 1 следует, что элементы второго столбца нового определителя (равного $\Delta(x)$) при разложении в ряд Маклорена начинаются со степени как минимум $2N+2$. Поэтому $\Delta(x)=Ax^{2N+2}$, $A\ne0$ $\qed$.
Пусть $m=\lfloor e^n\rfloor$, $e^n=m+\delta$. Для краткости обозначим $F_r(z)=F_r(z,1)$. Тогда Лемма 1 даёт

$$F_r(0)\delta=F_r(n)-mF_r(0)+e^{n}\int_0^nf_r(t)e^{-t}dt.$$

Из Леммы 2 следует, что хотя бы одно из двух целых чисел $F_r(n)-mF_r(0)$ не равно $0$. Тогда при этом $r$ получаем

$$|F_r(0)|\delta\geqslant1-e^{n}\int_0^nf_r(t)e^{-t}dt,$$

откуда получаем оценку снизу для $\delta$ (вот здесь надо выбирать $N$, оптимальный выбор - нечто вроде $N\asymp n^2$). Осталось выбрать $k(n)$ таким образом, чтобы остаток ряда был меньше $\delta$. Думаю, что это Вы сами в состоянии проделать.

Добавлено спустя 1 час 18 минут 24 секунды:

В книжке Фельдман Н.И. — Седьмая проблема Гильберта можно почитать, как этот метод работает в более общей ситуации.