Доброго времени суток! Помогите, пожалуйста, разобраться.
1) Найти длину кривой, ограниченной

.
Правильно ли я составил интеграл?

2) Исследовать функцию

на непрерывность в точке

Преподаватель сказал, что нужно расписать на языке эпислон-дельта.
Я понимаю, что функция будет непрерывна в начале координат, если
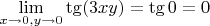
.
Тогда нужно, чтобы

должно


для точек, удовлетворяющих

выполнялось неравенство

.
Но такую зависимость

мне не придумать.
И еще возникает у нас ограничение

для целых

. Видимо это нужно учесть как-то, чтобы дельта окрестность не залезла в область, где функция не определена.
Как ограничить тангенс - ума не приложу... В правильном ли я направлении?