Из этого условия следует, что , если ряд

сходится, то последовательность
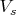
стремится к 0 со скоростью геометрической прогрессии (или быстрее) для любых

.
Отсюда, в свою очередь, следует, что последовательность
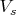
не может стремиться к 0, например, как

( это медленнее, чем геометрическая прогрессия), потому что соответствующий ряд

сходится, и мы получим противоречие с предыдущим утверждением.
Остается неясным, что будет, если ряд

расходится.