А откуда тут элементарные преобразования? Матрицы, отличающиеся на элементарное преобразование - это разные матрицы.
Да это я так с бухты барахты написал. Наверное корректно будет что нибудь вроде этого. Пусть пространство

определяется элементами с точность до гомеоморфизма или изоморфизма. Пусть отображение

- взаимно-однозначное отображение из пространства

в множество матриц. Определим обратное отображение

. Из свойств биекции будет следовать, что

определено и определено корректно с точностью до гомеоморфизма.
-- 25.02.2019, 15:38 --Пусть отображение
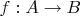
является биекцией. Из свойств биекции следует, что существует и единственно отображение

, такое что

. Такое отображение

будем называть обратным к

.
Спасибо! Как это всё доказать на строгом уровне? Достаточно показать, что существует биекция, а из этого будет следовать остальное?