Всем привет, прошу помощи:
1) Если

имеет первообразную

, можно ли утверждать, что

?
2) Верно ли, что функция, имеющая точку разрыва второго рода, не имеет первообразной (на том же интервале, разумеется)?
Вопросы пошли из простой задачи:
Показать что

не имеет первообразной.
Собственно первообразная должна была бы быть дифференцируемой в каждой точке интервала, но левый и правый предел в
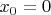
не существуют, хотя функция определена.