Лагранжевы координаты

[Sicker]

DimaM в сообщении #1376092 писал(а):

Понял проблему. Скорость задана в целых точках, а плотность в полуцелых.

Я тоже думал об этом, а это разве проблема? В уравнении газодинамики так же, все внутренние характеристики - плотность, давление, энергия все в полуцелых. Это вроде называется схема креста.

Pavia в сообщении #1376097 писал(а):

Так что переносить скорость влево ну никак не получается.

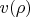
Я тоже об этом думал, только сразу возникает два вопроса. Во-первых, тогда получается что скорость распространения направлена вправо, и не зависит от вида $v(\rho)$. И во-вторых, ведь скорости различаются на малую величину, почему их нельзя смещать?

[Red_Herring]

Sicker в сообщении #1376217 писал(а):

В уравнении газодинамики

То что вы пишете не уравнение газодинамики, а разностная схема, которая, предположительно, его "решает".

[Sicker]

Red_Herring в сообщении #1376226 писал(а):

То что вы пишете не уравнение газодинамики, а разностная схема, которая, предположительно, его "решает".

Ну да, я думал это очевидно Только не предположительно, а решает.

[SergeyGubanov]

Geen в сообщении #1375848 писал(а):

Red_Herring в сообщении #1375828 писал(а):

Но "Эйлерово" уравнение расписывается как

А можно в ещё "более ковариантном" виде (неоднородное)?

$$ \frac{1}{\sqrt{g}}\frac{\partial \sqrt{g} J^{\mu}}{\partial x^{\mu}} = 0 $$

$$ J^{\mu} \frac{\partial}{\partial x^{\mu}} = \rho \frac{\partial}{\partial t} + \rho \left( v^i - V^i \right) \frac{\partial}{\partial x^{i}} $$

[Red_Herring]

Sicker в сообщении #1376231 писал(а):

Только не предположительно, а решает.

И даже при разрывных решениях? Что-то сомневаюсь (из-за неуместных прыжков и плясок с целыми и нецелыми). И тот, кто вам преподавал "вычислительную физику" видел ли в своей жизни доказательство сходимости этой схемы?

[Sicker]

Red_Herring в сообщении #1376285 писал(а):

И даже при разрывных решениях?

Я помню, мы как раз разрывную схему и рассматривали. При скачке давления. Хотя там вроде еще были танцы с бубном) Там искусственную вязкость вроде вводили, и шаг по времени уменьшали.

[Pphantom]

Red_Herring в сообщении #1376285 писал(а):

И даже при разрывных решениях? Что-то сомневаюсь (из-за неуместных прыжков и плясок с целыми и нецелыми).

Sicker в сообщении #1376291 писал(а):

Там искусственную вязкость вроде вводили, и шаг по времени уменьшали.

Для явных схем второго порядка (а "квадрат" таковой является) эти танцы с бубном помогут слабо, поскольку они не являются монотонными. Red_Herring сомневается совершенно правильно - при быстрых перепадах плотности это все быстро развалится, и искусственная вязкость (которая сделает быстрый перепад из разрыва) не поможет.

[Sicker]

Pphantom
Ну да, нам это тоже не особо помогало, уже не помню как у кого получилось, но мучились мы долго
А кстати, как из вашего уравнения в лагранжевых координатах следует зависимость направления распространения волн возмущений от вида $v(\rho)$? Просто у меня такое же уравнение, только я что-то не вижу как.

[Pphantom]

Sicker в сообщении #1376429 писал(а):

А кстати, как из вашего уравнения в лагранжевых координатах следует зависимость направления распространения волн возмущений от вида $v(\rho)$?

Никак. Вам же уже писали:

DimaM в сообщении #1375942 писал(а):

Из одного уравнения неразрывности больше ничего извлечь нельзя.
Чтобы говорить про волны, необходимо еще дифф. уравнение для скорости (уравнение импульса).

[Sicker]

Pphantom
Да, точно! Я забыл дописать, что еще надо добавить зависимость скорости от плотности $v=c(\rho)$. Думал вы это по умолчанию имели ввиду. Теперь то все норм?

[Red_Herring]

Если есть разрывы, то уравнение в л.к. теряет смысл. Период. Известно, что для некоторых квазилинейных уравнений даже предельное решение (при "коэффициенте вязкости" стремящемся к нулю) может зависеть от вида этой вязкости (я помню из лекций почти 50 летней давности С.К.Годунова).

Поэтому что есть: (1) Уравнение в дивергентной форме в эйлеровых координатах ; (2) поскольку в классе разрывных решений появляются физически неоправданные решения типа ударных волн разрежения (типа, есть непрерывное локальное решение, а кроме него еще и разрывные), то появляется "условие диссипации", которое и препятствует появлению таких решений.

[Pphantom]

Sicker в сообщении #1376433 писал(а):

Теперь то все норм?

Теперь можно нормально сформулировать решаемую задачу. Пока есть какие-то бессистемные обрывки.

[Sicker]

Pphantom в сообщении #1376438 писал(а):

Теперь можно нормально сформулировать решаемую задачу. Пока есть какие-то бессистемные обрывки.

Собственно, в какую сторону распространяются волны возмущений

[DimaM]

Red_Herring в сообщении #1376437 писал(а):

2) поскольку в классе разрывных решений появляются физически неоправданные решения типа ударных волн разрежения (типа, есть непрерывное локальное решение, а кроме него еще и разрывные), то появляется "условие диссипации", которое и препятствует появлению таких решений

Разрывные решения (математики их, няп, зовут обобщенными) тоже вполне имеют право на жизнь.

-- 16.02.2019, 20:03 --

Sicker в сообщении #1376443 писал(а):

Собственно, в какую сторону распространяются волны возмущений

Нужно найти характеристики вашего уравнения - вдоль них и будут распространяться.

[Sicker]

DimaM в сообщении #1376445 писал(а):

Нужно найти характеристики вашего уравнения - вдоль них и будут распространяться.

Так уравнение нелинейное