oleg_telegаха.
И что же мы имеем из физики? А из физики мы имеем:
а) Второе правило Кирхгофа, которое отражает потенциальность электрического поля - разница потенциалов при обходе по замкнутому контуру равна нулю.
Это именно правило, а не закон (как меня учили много лет назад

), так как является приближением.
Оно верно при стационарном (не изменяющемся) магнитном поле. Но ток-то у нас меняется, а значит меняется магнитное поле!
Но в приближении, когда

(

- характерный размер схемы,

- характерное время протекающих процессов) и контур не находится в меняющемся внешнем поле, его можно считать верным.
б)

- заряд на конденсаторе прямо пропорционален напряжению на нем, а коэффициент пропорциональности называется ёмкость.
в)

- напряжение (падение напряжения) на активном сопротивлении прямо пропорционально току, закон Ома.
едем дальше.
1. СтОит обратить внимание, что

имеет размерность времени и называется
постоянная времени RC-цепочки.
2. Из найденного выражения для

можно найти
а) Напряжение на резисторе:

(постоянную интегрирования я обозначил

, вместо

)
б) Напряжение на конденсаторе:

3. Вы справедливо отметили, что наши выкладки верны если

. Но рассмотрим момент включения ключа

.
а) В этот момент ЭДС моментально становится равной

и далее остаётся постоянной. То есть наши выкладки справедливы для времени

.
б) При этом конденсатор в этот момент времени разряжен (
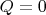
).
Вопрос: можете, исходя из этого, найти

?