сумма с корнями из единицы

[maxal]

Для всякого натурального $n$ докажите:

$$\sum_{k=1}^{2n+1}\frac{(-1)^k\omega^{\frac{k(3k+1)}{2}}}{1-\omega^{3k}}=-\frac{n+1}{2},$$

где $\omega$ - это примитивный корень степени $3n+2$ из единицы.

[nnosipov]

Сумма интересна тем, что ее значение не зависит от выбора примитивного корня, и эта независимость нетривиальна (при замене одного примитивного корня другим меняется состав слагаемых, а не, как это бывает в обычных тригонометрических тождествах, слагаемые просто переставляются). Ниже я приведу свое частичное (недо)решение, поскольку его идея никак не пересекается с идеей оригинального решения, но, в принципе, может быть полезна как технический прием. 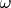Далее вместо $\omega$ используется буква $\zeta$. Предполагается, что число $3n+2$ --- простое, а искомое значение суммы является рациональным числом (что, конечно, a priori неочевидно).

Заметим, что если $k+l=2n+1$, то

$$ \zeta^{k(3k+1)/2}=\zeta^{l(3l+1)/2}, \quad \zeta^{3k}=\zeta^{-3l-1}. $$

В частности, имеем

$$ \sum_{k=1}^{2n+1}(-1)^k\zeta^{k(3k+1)/2}=-\sum_{l=0}^{2n}(-1)^l\zeta^{l(3l+1)/2}=-1. $$

Следовательно,

$$ \sum_{k=1}^{2n+1}(-1)^k\,\frac{\zeta^{k(3k+1)/2}}{1-\zeta^{3k}}= -\sum_{l=0}^{2n}(-1)^l\,\frac{\zeta^{l(3l+1)/2}}{1-\zeta^{-3l-1}}= \sum_{l=0}^{2n}(-1)^l\,\frac{\zeta^{l(3l+1)/2}}{1-\zeta^{3l+1}}-1. $$

Далее вычислим сумму

$$ S=\sum_{l=0}^{2n}(-1)^l\,\frac{\zeta^{l(3l+1)/2}}{1-\zeta^{3l+1}} $$

при условии, что $N=3n+2$ --- простое число, а $S$ --- рациональное число. При сделанных предположениях

$$ \sum_{l=0}^{2n}(-1)^l\,\frac{\zeta^{l(3l+1)j/2}}{1-\zeta^{(3l+1)j}}=S \eqno(*) $$

для любого $j=1,\,2,\,\dots,\,N-1$ (можно привлечь автоморфизм $\phi:\mathbb{Q}(\zeta) \to \mathbb{Q}(\zeta)$, заданный условием $\phi(\zeta)=\zeta^j$). Также заметим, что для любого натурального $N$ верны равенства

$$ \sum_{j=1}^{N-1}\frac{\zeta^{mj}}{1-\zeta^j}=-\frac{N+1}{2}+m \quad (m=1,\,2,\,\dots,\,N). $$

Для доказательства можно воспользоваться стандартным способом вычисления подобных тригонометрических сумм.

Просуммировав равенства $(*)$, получим

$$ (N-1)S=\sum_{j=1}^{N-1}\sum_{l=0}^{2n}(-1)^l\,\frac{\zeta^{l(3l+1)j/2}}{1-\zeta^{(3l+1)j}}= \sum_{l=0}^{2n}(-1)^l\sum_{j=1}^{N-1}\frac{\zeta^{l(3l+1)j/2}}{1-\zeta^{(3l+1)j}}. $$

Поскольку $\gcd{(3l+1,N)}=1$ при $0 \leqslant l \leqslant 2n$, имеем

$$ \sum_{j=1}^{N-1}\frac{\zeta^{l(3l+1)j/2}}{1-\zeta^{(3l+1)j}}= \sum_{j=1}^{N-1}\frac{\zeta^{m_lj}}{1-\zeta^j}=-\frac{N+1}{2}+m_l, $$

где целые числа $m_l$ удовлетворяют условиям

$$ m_l \equiv l/2 \pmod{N}, \quad 1 \leqslant m_l \leqslant N. $$

Следовательно,

$$ (N-1)S=\sum_{l=0}^{2n}(-1)^l\left(-\frac{N+1}{2}+m_l\right). \eqno(**) $$

Ясно, что $m_0=N$, а при $s=1,\,2,\,\dots,\,n$ имеем

$$ m_{2s-1}=\frac{N-1}{2}+s, \quad m_{2s}=s. $$

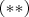
Теперь сумму в правой части равенства $(**)$ легко вычислить:

$$ \sum_{l=0}^{2n}(-1)^l\left(-\frac{N+1}{2}+m_l\right)= $$

$$ =\frac{N-1}{2}+\sum_{s=1}^n\left(-\frac{N+1}{2}+m_{2s}\right)- \sum_{s=1}^n\left(-\frac{N+1}{2}+m_{2s-1}\right)= $$

$$ =\frac{N-1}{2}+\sum_{s=1}^n(m_{2s}-m_{2s-1})=-\frac{(N-1)(n-1)}{2}. $$

В итого получим

$$ (N-1)S=-\frac{(N-1)(n-1)}{2}, $$

откуда и следует нужная формула для $S$.