Ну, и если она выпуклая, то, поскольку нужен алгоритм, я бы его составил простым перебором, а именно, перебирая точки кривой с некоторым шажком

.
Кривая задана, например, параметрическим уравнением

(или пусть даже дискретно-точечной тобличкой). В каждую точку

помещаем вершину

прямоугольника

, вычисляем точку

, куда встанет вершина

, определяем положения точек

и

(справа или слева от отрезка
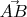
, в зависимости от направления обхода), и, наконец, определяем --- попали ли эти две точки внутрь фигуры.
Повторяем цикл до первой удачи.
Это тупое решение на скорую руку, солнце и суббота мешают и гонят подальше от ЭВМ...