Всех с прошедшими праздниками. Помогите разобраться. Задача: В ориентированном графе 101 вершина. У каждой вершины число входящих и число выходящих ребер равно 40. Доказать, что из любой вершины можно попасть в любую, проходя не более чем по трём ребрам.
Изобразил ситуацию на на рис., кружкАми обозначены вершины графа.

Решение автора: Пусть

– две вершины данного графа,

– множество из

вершин, в которые ведут рёбра из

,

– множество из

вершин, из которых идут рёбра в

,

– множество из 19 оставшихся вершин.
Предположим, что из

нельзя пройти в
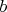
по трём рёбрам. Тогда все рёбра, выходящие из

, идут в

или в

. Этих рёбер по условию всего

. Но рёбер внутри

не больше, чем

, а рёбер, которые могут прийти из

в

не больше чем

, что в сумме даёт

. Полученное противоречие опровергает сделанное предположение. Значит, из любой вершины можно попасть в любую, проходя не более чем по трём рёбрам.
Вроде это понятно. Не понятно, почему утверждается, что ребер внутри

не больше, чем

, а не:

? Или такая ситуация не допустима (см.ниже) ?
