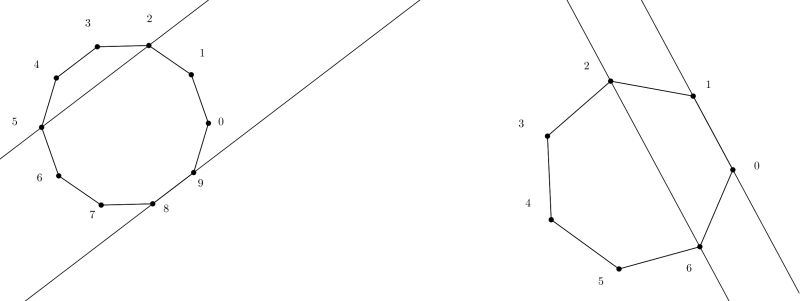
Я думаю, что задача определения числа параллельных пар отрезков, концы которых являются вершинами правильного

- угольника, хорошо известна и уже давно решена.
Я решил применить аппарат комплексных чисел для решения данной задачи. Я пронумеровал вершины правильного

угольника числами из множества
![$W= \[\left\{ {0,1,2,...,(n-1)} \right\}\]$ $W= \[\left\{ {0,1,2,...,(n-1)} \right\}\]$](https://dxdy-03.korotkov.co.uk/f/6/3/a/63aec98724980d29d4e2d6e75b9f883c82.png)
, и поставил им в соответствие комплексные числа
![$\[\cos \frac{{2\pi k}}{n} + i\sin \frac{{2\pi k}}{n}\]$ $\[\cos \frac{{2\pi k}}{n} + i\sin \frac{{2\pi k}}{n}\]$](https://dxdy-01.korotkov.co.uk/f/0/c/5/0c533dc50998b835a83a02cc822348db82.png)
,
![$\[k \in W\]$ $\[k \in W\]$](https://dxdy-03.korotkov.co.uk/f/6/8/2/682f95e1ef6ac945e924a0cc4d5b444982.png)
. Далее я рассматриваю попарно неравные числа
![$\[{i_1},{i_2},{j_1},{j_2} \in W\]$ $\[{i_1},{i_2},{j_1},{j_2} \in W\]$](https://dxdy-01.korotkov.co.uk/f/c/c/5/cc50e2bef660b7632afee892ab13572282.png)
, и ставлю им в соответствие комплексные числа
![$$\[\begin{array}{l}
{z_{{i_1}}} = \cos \frac{{2\pi {i_1}}}{n} + i\sin \frac{{2\pi {i_1}}}{n};{z_{{i_2}}} = \cos \frac{{2\pi {i_2}}}{n} + i\sin \frac{{2\pi {i_2}}}{n}\\
{z_{{j_1}}} = \cos \frac{{2\pi {j_1}}}{n} + i\sin \frac{{2\pi {j_1}}}{n};{z_{{j_2}}} = \cos \frac{{2\pi {j_2}}}{n} + i\sin \frac{{2\pi {j_2}}}{n}
\end{array}\]$$ $$\[\begin{array}{l}
{z_{{i_1}}} = \cos \frac{{2\pi {i_1}}}{n} + i\sin \frac{{2\pi {i_1}}}{n};{z_{{i_2}}} = \cos \frac{{2\pi {i_2}}}{n} + i\sin \frac{{2\pi {i_2}}}{n}\\
{z_{{j_1}}} = \cos \frac{{2\pi {j_1}}}{n} + i\sin \frac{{2\pi {j_1}}}{n};{z_{{j_2}}} = \cos \frac{{2\pi {j_2}}}{n} + i\sin \frac{{2\pi {j_2}}}{n}
\end{array}\]$$](https://dxdy-03.korotkov.co.uk/f/6/9/d/69d08f6a6678c08628b51c10c7cd7fda82.png)
Определим вектора
![$\[\overrightarrow {{r_{{i_1}{j_1}}}} = {z_{{i_1}}} - {z_{{j_1}}}\]$ $\[\overrightarrow {{r_{{i_1}{j_1}}}} = {z_{{i_1}}} - {z_{{j_1}}}\]$](https://dxdy-04.korotkov.co.uk/f/3/a/b/3ab8c9cdd4e40a402e565da5d6c573f982.png)
и
![$\[\overrightarrow {{r_{{i_2}{j_2}}}} = {z_{{i_2}}} - {z_{{j_2}}}\]$ $\[\overrightarrow {{r_{{i_2}{j_2}}}} = {z_{{i_2}}} - {z_{{j_2}}}\]$](https://dxdy-01.korotkov.co.uk/f/0/a/6/0a6e8b6bf1e2e56af5856edc64c51c8b82.png)
. Будем искать количество четверок

, удовлетворяющих условию
![$\[\overrightarrow {{r_{{i_1}{j_1}}}} \parallel \overrightarrow {{r_{{i_2}{j_2}}}} \]$ $\[\overrightarrow {{r_{{i_1}{j_1}}}} \parallel \overrightarrow {{r_{{i_2}{j_2}}}} \]$](https://dxdy-02.korotkov.co.uk/f/d/3/0/d30b34621c35f5758b224d402853156082.png)
. Это количество будет в

раза больше количества пар отрезков, удовлетворяющих условию задачи, поскольку можно, меняя направления векторов, получить

пар коллинеарных векторов, которые будут удовлетворять
![$\[\overrightarrow {{r_{{i_1}{j_1}}}} \parallel \overrightarrow {{r_{{i_2}{j_2}}}} \]$ $\[\overrightarrow {{r_{{i_1}{j_1}}}} \parallel \overrightarrow {{r_{{i_2}{j_2}}}} \]$](https://dxdy-02.korotkov.co.uk/f/d/3/0/d30b34621c35f5758b224d402853156082.png)
и которые будут задавать только одну пару параллельных отрезков. Условие
![$\[\overrightarrow {{r_{{i_1}{j_1}}}} \parallel \overrightarrow {{r_{{i_2}{j_2}}}} \]$ $\[\overrightarrow {{r_{{i_1}{j_1}}}} \parallel \overrightarrow {{r_{{i_2}{j_2}}}} \]$](https://dxdy-02.korotkov.co.uk/f/d/3/0/d30b34621c35f5758b224d402853156082.png)
равносильно
![$$
\[\frac{{{z_{{i_1}}} - {z_{{j_1}}}}}{{{z_{{i_2}}} - {z_{{j_2}}}}} = \frac{{\overline {{z_{{i_1}}}} - \overline {{z_{{j_1}}}} }}{{\overline {{z_{{i_2}}}} - \overline {{z_{{j_2}}}} }}\]$$ $$
\[\frac{{{z_{{i_1}}} - {z_{{j_1}}}}}{{{z_{{i_2}}} - {z_{{j_2}}}}} = \frac{{\overline {{z_{{i_1}}}} - \overline {{z_{{j_1}}}} }}{{\overline {{z_{{i_2}}}} - \overline {{z_{{j_2}}}} }}\]$$](https://dxdy-02.korotkov.co.uk/f/5/2/3/52372c937b3814f1b51ae567b22a46f582.png)
Будем преобразовывать это выражение:
![$$
\[\begin{array}{l}
\frac{{\left( {\cos \frac{{2\pi {i_1}}}{n} + i\sin \frac{{2\pi {i_1}}}{n}} \right) - \left( {\cos \frac{{2\pi {j_1}}}{n} + i\sin \frac{{2\pi {j_1}}}{n}} \right)}}{{\left( {\cos \frac{{2\pi {i_2}}}{n} + i\sin \frac{{2\pi {i_2}}}{n}} \right) - \left( {\cos \frac{{2\pi {j_2}}}{n} + i\sin \frac{{2\pi {j_2}}}{n}} \right)}} = \frac{{\left( {\cos \frac{{2\pi {i_1}}}{n} - i\sin \frac{{2\pi {i_1}}}{n}} \right) - \left( {\cos \frac{{2\pi {j_1}}}{n} - i\sin \frac{{2\pi {j_1}}}{n}} \right)}}{{\left( {\cos \frac{{2\pi {i_2}}}{n} - i\sin \frac{{2\pi {i_2}}}{n}} \right) - \left( {\cos \frac{{2\pi {j_2}}}{n} - i\sin \frac{{2\pi {j_2}}}{n}} \right)}} \Leftrightarrow \\
\\
\\
\frac{{\left( {\cos \frac{{2\pi {i_1}}}{n} - \cos \frac{{2\pi {j_1}}}{n}} \right) + i\left( {\sin \frac{{2\pi {i_1}}}{n} - \sin \frac{{2\pi {j_1}}}{n}} \right)}}{{\left( {\cos \frac{{2\pi {i_2}}}{n} - \cos \frac{{2\pi {j_2}}}{n}} \right) + i\left( {\sin \frac{{2\pi {i_2}}}{n} - \sin \frac{{2\pi {j_2}}}{n}} \right)}} = \frac{{\left( {\cos \frac{{2\pi {i_1}}}{n} - \cos \frac{{2\pi {j_1}}}{n}} \right) - i\left( {\sin \frac{{2\pi {i_1}}}{n} - \sin \frac{{2\pi {j_1}}}{n}} \right)}}{{\left( {\cos \frac{{2\pi {i_2}}}{n} - \cos \frac{{2\pi {j_2}}}{n}} \right) - i\left( {\sin \frac{{2\pi {i_2}}}{n} - \sin \frac{{2\pi {j_2}}}{n}} \right)}} \Leftrightarrow \\
\\
\\
\frac{{ - 2\sin \frac{{\pi \left( {{i_1} - {j_1}} \right)}}{n}\sin \frac{{\pi \left( {{i_1} + {j_1}} \right)}}{n} + i\left( {2\sin \frac{{\pi \left( {{i_1} - {j_1}} \right)}}{n}\cos \frac{{\pi \left( {{i_1} + {j_1}} \right)}}{n}} \right)}}{{ - 2\sin \frac{{\pi \left( {{i_2} - {j_2}} \right)}}{n}\sin \frac{{\pi \left( {{i_2} + {j_2}} \right)}}{n} + i\left( {2\sin \frac{{\pi \left( {{i_2} - {j_2}} \right)}}{n}\cos \frac{{\pi \left( {{i_2} + {j_2}} \right)}}{n}} \right)}} = \frac{{ - 2\sin \frac{{\pi \left( {{i_1} - {j_1}} \right)}}{n}\sin \frac{{\pi \left( {{i_1} + {j_1}} \right)}}{n} - i\left( {2\sin \frac{{\pi \left( {{i_1} - {j_1}} \right)}}{n}\cos \frac{{\pi \left( {{i_1} + {j_1}} \right)}}{n}} \right)}}{{ - 2\sin \frac{{\pi \left( {{i_2} - {j_2}} \right)}}{n}\sin \frac{{\pi \left( {{i_2} + {j_2}} \right)}}{n} - i\left( {2\sin \frac{{\pi \left( {{i_2} - {j_2}} \right)}}{n}\cos \frac{{\pi \left( {{i_2} + {j_2}} \right)}}{n}} \right)}} \Leftrightarrow \\
\\
\\
\frac{{\sin \frac{{\pi \left( {{i_1} - {j_1}} \right)}}{n}\sin \frac{{\pi \left( {{i_1} + {j_1}} \right)}}{n} - i\sin \frac{{\pi \left( {{i_1} - {j_1}} \right)}}{n}\cos \frac{{\pi \left( {{i_1} + {j_1}} \right)}}{n}}}{{\sin \frac{{\pi \left( {{i_2} - {j_2}} \right)}}{n}\sin \frac{{\pi \left( {{i_2} + {j_2}} \right)}}{n} - i\sin \frac{{\pi \left( {{i_2} - {j_2}} \right)}}{n}\cos \frac{{\pi \left( {{i_2} + {j_2}} \right)}}{n}}} = \frac{{\sin \frac{{\pi \left( {{i_1} - {j_1}} \right)}}{n}\sin \frac{{\pi \left( {{i_1} + {j_1}} \right)}}{n} + i\sin \frac{{\pi \left( {{i_1} - {j_1}} \right)}}{n}\cos \frac{{\pi \left( {{i_1} + {j_1}} \right)}}{n}}}{{\sin \frac{{\pi \left( {{i_2} - {j_2}} \right)}}{n}\sin \frac{{\pi \left( {{i_2} + {j_2}} \right)}}{n} + i\sin \frac{{\pi \left( {{i_2} - {j_2}} \right)}}{n}\cos \frac{{\pi \left( {{i_2} + {j_2}} \right)}}{n}}}
\end{array}\]$$ $$
\[\begin{array}{l}
\frac{{\left( {\cos \frac{{2\pi {i_1}}}{n} + i\sin \frac{{2\pi {i_1}}}{n}} \right) - \left( {\cos \frac{{2\pi {j_1}}}{n} + i\sin \frac{{2\pi {j_1}}}{n}} \right)}}{{\left( {\cos \frac{{2\pi {i_2}}}{n} + i\sin \frac{{2\pi {i_2}}}{n}} \right) - \left( {\cos \frac{{2\pi {j_2}}}{n} + i\sin \frac{{2\pi {j_2}}}{n}} \right)}} = \frac{{\left( {\cos \frac{{2\pi {i_1}}}{n} - i\sin \frac{{2\pi {i_1}}}{n}} \right) - \left( {\cos \frac{{2\pi {j_1}}}{n} - i\sin \frac{{2\pi {j_1}}}{n}} \right)}}{{\left( {\cos \frac{{2\pi {i_2}}}{n} - i\sin \frac{{2\pi {i_2}}}{n}} \right) - \left( {\cos \frac{{2\pi {j_2}}}{n} - i\sin \frac{{2\pi {j_2}}}{n}} \right)}} \Leftrightarrow \\
\\
\\
\frac{{\left( {\cos \frac{{2\pi {i_1}}}{n} - \cos \frac{{2\pi {j_1}}}{n}} \right) + i\left( {\sin \frac{{2\pi {i_1}}}{n} - \sin \frac{{2\pi {j_1}}}{n}} \right)}}{{\left( {\cos \frac{{2\pi {i_2}}}{n} - \cos \frac{{2\pi {j_2}}}{n}} \right) + i\left( {\sin \frac{{2\pi {i_2}}}{n} - \sin \frac{{2\pi {j_2}}}{n}} \right)}} = \frac{{\left( {\cos \frac{{2\pi {i_1}}}{n} - \cos \frac{{2\pi {j_1}}}{n}} \right) - i\left( {\sin \frac{{2\pi {i_1}}}{n} - \sin \frac{{2\pi {j_1}}}{n}} \right)}}{{\left( {\cos \frac{{2\pi {i_2}}}{n} - \cos \frac{{2\pi {j_2}}}{n}} \right) - i\left( {\sin \frac{{2\pi {i_2}}}{n} - \sin \frac{{2\pi {j_2}}}{n}} \right)}} \Leftrightarrow \\
\\
\\
\frac{{ - 2\sin \frac{{\pi \left( {{i_1} - {j_1}} \right)}}{n}\sin \frac{{\pi \left( {{i_1} + {j_1}} \right)}}{n} + i\left( {2\sin \frac{{\pi \left( {{i_1} - {j_1}} \right)}}{n}\cos \frac{{\pi \left( {{i_1} + {j_1}} \right)}}{n}} \right)}}{{ - 2\sin \frac{{\pi \left( {{i_2} - {j_2}} \right)}}{n}\sin \frac{{\pi \left( {{i_2} + {j_2}} \right)}}{n} + i\left( {2\sin \frac{{\pi \left( {{i_2} - {j_2}} \right)}}{n}\cos \frac{{\pi \left( {{i_2} + {j_2}} \right)}}{n}} \right)}} = \frac{{ - 2\sin \frac{{\pi \left( {{i_1} - {j_1}} \right)}}{n}\sin \frac{{\pi \left( {{i_1} + {j_1}} \right)}}{n} - i\left( {2\sin \frac{{\pi \left( {{i_1} - {j_1}} \right)}}{n}\cos \frac{{\pi \left( {{i_1} + {j_1}} \right)}}{n}} \right)}}{{ - 2\sin \frac{{\pi \left( {{i_2} - {j_2}} \right)}}{n}\sin \frac{{\pi \left( {{i_2} + {j_2}} \right)}}{n} - i\left( {2\sin \frac{{\pi \left( {{i_2} - {j_2}} \right)}}{n}\cos \frac{{\pi \left( {{i_2} + {j_2}} \right)}}{n}} \right)}} \Leftrightarrow \\
\\
\\
\frac{{\sin \frac{{\pi \left( {{i_1} - {j_1}} \right)}}{n}\sin \frac{{\pi \left( {{i_1} + {j_1}} \right)}}{n} - i\sin \frac{{\pi \left( {{i_1} - {j_1}} \right)}}{n}\cos \frac{{\pi \left( {{i_1} + {j_1}} \right)}}{n}}}{{\sin \frac{{\pi \left( {{i_2} - {j_2}} \right)}}{n}\sin \frac{{\pi \left( {{i_2} + {j_2}} \right)}}{n} - i\sin \frac{{\pi \left( {{i_2} - {j_2}} \right)}}{n}\cos \frac{{\pi \left( {{i_2} + {j_2}} \right)}}{n}}} = \frac{{\sin \frac{{\pi \left( {{i_1} - {j_1}} \right)}}{n}\sin \frac{{\pi \left( {{i_1} + {j_1}} \right)}}{n} + i\sin \frac{{\pi \left( {{i_1} - {j_1}} \right)}}{n}\cos \frac{{\pi \left( {{i_1} + {j_1}} \right)}}{n}}}{{\sin \frac{{\pi \left( {{i_2} - {j_2}} \right)}}{n}\sin \frac{{\pi \left( {{i_2} + {j_2}} \right)}}{n} + i\sin \frac{{\pi \left( {{i_2} - {j_2}} \right)}}{n}\cos \frac{{\pi \left( {{i_2} + {j_2}} \right)}}{n}}}
\end{array}\]$$](https://dxdy-04.korotkov.co.uk/f/b/2/2/b229ba436da69c59227e8abae15664e882.png)
Сделаем замены:
![$$\[\begin{array}{l}
A = \sin \frac{{\pi \left( {{i_1} - {j_1}} \right)}}{n}\sin \frac{{\pi \left( {{i_1} + {j_1}} \right)}}{n};B = \sin \frac{{\pi \left( {{i_1} - {j_1}} \right)}}{n}\cos \frac{{\pi \left( {{i_1} + {j_1}} \right)}}{n}\\
C = \sin \frac{{\pi \left( {{i_2} - {j_2}} \right)}}{n}\sin \frac{{\pi \left( {{i_2} + {j_2}} \right)}}{n};D = \sin \frac{{\pi \left( {{i_2} - {j_2}} \right)}}{n}\cos \frac{{\pi \left( {{i_2} + {j_2}} \right)}}{n}
\end{array}\]$$ $$\[\begin{array}{l}
A = \sin \frac{{\pi \left( {{i_1} - {j_1}} \right)}}{n}\sin \frac{{\pi \left( {{i_1} + {j_1}} \right)}}{n};B = \sin \frac{{\pi \left( {{i_1} - {j_1}} \right)}}{n}\cos \frac{{\pi \left( {{i_1} + {j_1}} \right)}}{n}\\
C = \sin \frac{{\pi \left( {{i_2} - {j_2}} \right)}}{n}\sin \frac{{\pi \left( {{i_2} + {j_2}} \right)}}{n};D = \sin \frac{{\pi \left( {{i_2} - {j_2}} \right)}}{n}\cos \frac{{\pi \left( {{i_2} + {j_2}} \right)}}{n}
\end{array}\]$$](https://dxdy-01.korotkov.co.uk/f/0/1/6/016439e248bc0e8f8f384e96a98d597f82.png)
тогда имеем
![$$
\[\begin{array}{l}
\frac{{A - iB}}{{C - iD}} = \frac{{A + iB}}{{C + iD}} \Leftrightarrow \left( {A - iB} \right)\left( {C + iD} \right) = \left( {A + iB} \right)\left( {C - iD} \right) \Leftrightarrow \\
AC + iAD - iBC - {i^2}BD = AC - iAD + iBC - {i^2}BD \Leftrightarrow AD = BC \Leftrightarrow \\
\sin \frac{{\pi \left( {{i_1} - {j_1}} \right)}}{n}\sin \frac{{\pi \left( {{i_1} + {j_1}} \right)}}{n}\sin \frac{{\pi \left( {{i_2} - {j_2}} \right)}}{n}\cos \frac{{\pi \left( {{i_2} + {j_2}} \right)}}{n} = \sin \frac{{\pi \left( {{i_1} - {j_1}} \right)}}{n}\cos \frac{{\pi \left( {{i_1} + {j_1}} \right)}}{n}\sin \frac{{\pi \left( {{i_2} - {j_2}} \right)}}{n}\sin \frac{{\pi \left( {{i_2} + {j_2}} \right)}}{n}\\
\sin \frac{{\pi \left( {{i_1} + {j_1}} \right)}}{n}\cos \frac{{\pi \left( {{i_2} + {j_2}} \right)}}{n} = \cos \frac{{\pi \left( {{i_1} + {j_1}} \right)}}{n}\sin \frac{{\pi \left( {{i_2} + {j_2}} \right)}}{n}
\end{array}\]
$$ $$
\[\begin{array}{l}
\frac{{A - iB}}{{C - iD}} = \frac{{A + iB}}{{C + iD}} \Leftrightarrow \left( {A - iB} \right)\left( {C + iD} \right) = \left( {A + iB} \right)\left( {C - iD} \right) \Leftrightarrow \\
AC + iAD - iBC - {i^2}BD = AC - iAD + iBC - {i^2}BD \Leftrightarrow AD = BC \Leftrightarrow \\
\sin \frac{{\pi \left( {{i_1} - {j_1}} \right)}}{n}\sin \frac{{\pi \left( {{i_1} + {j_1}} \right)}}{n}\sin \frac{{\pi \left( {{i_2} - {j_2}} \right)}}{n}\cos \frac{{\pi \left( {{i_2} + {j_2}} \right)}}{n} = \sin \frac{{\pi \left( {{i_1} - {j_1}} \right)}}{n}\cos \frac{{\pi \left( {{i_1} + {j_1}} \right)}}{n}\sin \frac{{\pi \left( {{i_2} - {j_2}} \right)}}{n}\sin \frac{{\pi \left( {{i_2} + {j_2}} \right)}}{n}\\
\sin \frac{{\pi \left( {{i_1} + {j_1}} \right)}}{n}\cos \frac{{\pi \left( {{i_2} + {j_2}} \right)}}{n} = \cos \frac{{\pi \left( {{i_1} + {j_1}} \right)}}{n}\sin \frac{{\pi \left( {{i_2} + {j_2}} \right)}}{n}
\end{array}\]
$$](https://dxdy-03.korotkov.co.uk/f/e/5/6/e56f8b2768cc98ed3ef5ded6d76704ff82.png)
Мы, таким образом, вывели равносильное условие коллинеарности векторов:
![$$\[\sin \frac{{\pi \left( {{i_1} + {j_1}} \right)}}{n}\cos \frac{{\pi \left( {{i_2} + {j_2}} \right)}}{n} = \cos \frac{{\pi \left( {{i_1} + {j_1}} \right)}}{n}\sin \frac{{\pi \left( {{i_2} + {j_2}} \right)}}{n}\]$$ $$\[\sin \frac{{\pi \left( {{i_1} + {j_1}} \right)}}{n}\cos \frac{{\pi \left( {{i_2} + {j_2}} \right)}}{n} = \cos \frac{{\pi \left( {{i_1} + {j_1}} \right)}}{n}\sin \frac{{\pi \left( {{i_2} + {j_2}} \right)}}{n}\]$$](https://dxdy-04.korotkov.co.uk/f/f/6/d/f6d35bf223519b0e497b75c2bbf5e36382.png)
Преобразуем его. Для этого сначала рассмотрим 2 случая:
Cлучай 1)
![$$\[\sin \frac{{\pi \left( {{i_2} + {j_2}} \right)}}{n} = \pm 1 \Leftrightarrow {i_2} + {j_2} = n + 2nk \Leftrightarrow \cos \frac{{\pi \left( {{i_2} + {j_2}} \right)}}{n} = 0\]$$ $$\[\sin \frac{{\pi \left( {{i_2} + {j_2}} \right)}}{n} = \pm 1 \Leftrightarrow {i_2} + {j_2} = n + 2nk \Leftrightarrow \cos \frac{{\pi \left( {{i_2} + {j_2}} \right)}}{n} = 0\]$$](https://dxdy-03.korotkov.co.uk/f/6/1/a/61a44b45a89b9c694ab81c90ea56588282.png)
Чтобы уравнение выполнялось, необходимо положить
![$$\[\cos \frac{{\pi \left( {{i_1} + {j_1}} \right)}}{n} = 0 \Leftrightarrow {i_1} + {j_1} = n + 2n{k_2}\]$$ $$\[\cos \frac{{\pi \left( {{i_1} + {j_1}} \right)}}{n} = 0 \Leftrightarrow {i_1} + {j_1} = n + 2n{k_2}\]$$](https://dxdy-04.korotkov.co.uk/f/7/7/5/7755323a21cb982e3f6979ca3201f84a82.png)
Таким образом, мы имеем систему:
![$$\[\left\{ \begin{array}{l}
{i_2} + {j_2} = n + 2n{k_1}\\
{i_1} + {j_1} = n + 2n{k_2}
\end{array} \right.\]$$ $$\[\left\{ \begin{array}{l}
{i_2} + {j_2} = n + 2n{k_1}\\
{i_1} + {j_1} = n + 2n{k_2}
\end{array} \right.\]$$](https://dxdy-01.korotkov.co.uk/f/4/4/f/44fffdea7c76d592623ad781bbd328ce82.png)
Максимум и минимум данных сумм равны соответственно
![$\[\left( {n - 1} \right) + \left( {n - 2} \right) = 2n - 3 < 3n\]$ $\[\left( {n - 1} \right) + \left( {n - 2} \right) = 2n - 3 < 3n\]$](https://dxdy-01.korotkov.co.uk/f/8/7/0/870773ee3cf4289f4542a2fd1a405c4882.png)
и
![$\[0 + 1 = 1 > - n\]$ $\[0 + 1 = 1 > - n\]$](https://dxdy-01.korotkov.co.uk/f/c/d/3/cd33d7777fea08720050f5fa31cd79df82.png)
, так что мы окончательно приходим к системе:
![$$\[\left\{ \begin{array}{l}
{i_2} + {j_2} = n \\
{i_1} + {j_1} = n
\end{array} \right.\]$$ $$\[\left\{ \begin{array}{l}
{i_2} + {j_2} = n \\
{i_1} + {j_1} = n
\end{array} \right.\]$$](https://dxdy-03.korotkov.co.uk/f/a/5/0/a501c710bd5791ef44b6e6ad7c0a712882.png)
Случай 2) Пусть теперь
![$\[{i_2} + {j_2} \ne n + 2n{k_1}\]$ $\[{i_2} + {j_2} \ne n + 2n{k_1}\]$](https://dxdy-02.korotkov.co.uk/f/d/0/0/d0041c9ae2f90ea4f98d8cc08dd0087782.png)
. Тогда можно смело делить уравнение на
![$\[\cos \frac{{\pi \left( {{i_1} + {j_1}} \right)}}{n}\sin \frac{{\pi \left( {{i_2} + {j_2}} \right)}}{n}\]$ $\[\cos \frac{{\pi \left( {{i_1} + {j_1}} \right)}}{n}\sin \frac{{\pi \left( {{i_2} + {j_2}} \right)}}{n}\]$](https://dxdy-03.korotkov.co.uk/f/2/b/4/2b4ce1d5b717d9f371d2f120082c060782.png)
:
![$$\[\begin{array}{l}
\tan \frac{{\pi \left( {{i_1} + {j_1}} \right)}}{n} = \tan \frac{{\pi \left( {{i_2} + {j_2}} \right)}}{n} \Leftrightarrow \frac{{\sin \left( {\frac{{\pi \left( {{i_1} + {j_1}} \right)}}{n} - \frac{{\pi \left( {{i_2} + {j_2}} \right)}}{n}} \right)}}{{\cos \frac{{\pi \left( {{i_1} + {j_1}} \right)}}{n}\cos \frac{{\pi \left( {{i_2} + {j_2}} \right)}}{n}}} = 0\mathop \Leftrightarrow \limits^{\cos \frac{{\pi \left( {{i_1} + {j_1}} \right)}}{n} \ne 0,\cos \frac{{\pi \left( {{i_2} + {j_2}} \right)}}{n} \ne 0} \\
\sin \left( {\frac{{\pi \left( {{i_1} + {j_1}} \right)}}{n} - \frac{{\pi \left( {{i_2} + {j_2}} \right)}}{n}} \right) = 0 \Leftrightarrow \frac{{\pi \left( {{i_1} + {j_1}} \right)}}{n} - \frac{{\pi \left( {{i_2} + {j_2}} \right)}}{n} = \pi {k_3} \Leftrightarrow \\
\left( {{i_1} + {j_1}} \right) - \left( {{i_2} + {j_2}} \right) = n{k_3}
\end{array}\]$$ $$\[\begin{array}{l}
\tan \frac{{\pi \left( {{i_1} + {j_1}} \right)}}{n} = \tan \frac{{\pi \left( {{i_2} + {j_2}} \right)}}{n} \Leftrightarrow \frac{{\sin \left( {\frac{{\pi \left( {{i_1} + {j_1}} \right)}}{n} - \frac{{\pi \left( {{i_2} + {j_2}} \right)}}{n}} \right)}}{{\cos \frac{{\pi \left( {{i_1} + {j_1}} \right)}}{n}\cos \frac{{\pi \left( {{i_2} + {j_2}} \right)}}{n}}} = 0\mathop \Leftrightarrow \limits^{\cos \frac{{\pi \left( {{i_1} + {j_1}} \right)}}{n} \ne 0,\cos \frac{{\pi \left( {{i_2} + {j_2}} \right)}}{n} \ne 0} \\
\sin \left( {\frac{{\pi \left( {{i_1} + {j_1}} \right)}}{n} - \frac{{\pi \left( {{i_2} + {j_2}} \right)}}{n}} \right) = 0 \Leftrightarrow \frac{{\pi \left( {{i_1} + {j_1}} \right)}}{n} - \frac{{\pi \left( {{i_2} + {j_2}} \right)}}{n} = \pi {k_3} \Leftrightarrow \\
\left( {{i_1} + {j_1}} \right) - \left( {{i_2} + {j_2}} \right) = n{k_3}
\end{array}\]$$](https://dxdy-02.korotkov.co.uk/f/9/c/0/9c0953651df0bf64db304f43bf91611282.png)
Максимум и минимум выражения

равны соответственно
![$\[\left( {(n - 1) + (n - 2)} \right) - \left( {0 + 1} \right) = 2n - 4 < 2n\]$ $\[\left( {(n - 1) + (n - 2)} \right) - \left( {0 + 1} \right) = 2n - 4 < 2n\]$](https://dxdy-04.korotkov.co.uk/f/f/5/9/f59e93026381d52120aabbd90a010b6782.png)
и
![$\[\left( {0 + 1} \right) - \left( {(n - 1) + (n - 2)} \right) = - 2n + 4 > 2n\]$ $\[\left( {0 + 1} \right) - \left( {(n - 1) + (n - 2)} \right) = - 2n + 4 > 2n\]$](https://dxdy-03.korotkov.co.uk/f/2/d/f/2df2d85e81224942beb10ed6172bc91882.png)
, так что получим совокупность
![$$
\[\left[ \begin{array}{l}
\left( {{i_1} + {j_1}} \right) - \left( {{i_2} + {j_2}} \right) = n\\
\left( {{i_1} + {j_1}} \right) - \left( {{i_2} + {j_2}} \right) = - n\\
\left( {{i_1} + {j_1}} \right) - \left( {{i_2} + {j_2}} \right) = 0
\end{array} \right.\]
$$ $$
\[\left[ \begin{array}{l}
\left( {{i_1} + {j_1}} \right) - \left( {{i_2} + {j_2}} \right) = n\\
\left( {{i_1} + {j_1}} \right) - \left( {{i_2} + {j_2}} \right) = - n\\
\left( {{i_1} + {j_1}} \right) - \left( {{i_2} + {j_2}} \right) = 0
\end{array} \right.\]
$$](https://dxdy-01.korotkov.co.uk/f/0/1/a/01a42b3d29a66fad88def30c05cb968282.png)
Итак, данная система равносильна следующей общей совокупности:
![$$\[\left[ \begin{array}{l}
\left\{ \begin{array}{l}
{i_1} + {j_1} = n\\
{i_2} + {j_2} = n
\end{array} \right.\\
\left\{ \begin{array}{l}
\left\{ \begin{array}{l}
{i_1} + {j_1} \ne n\\
{i_2} + {j_2} \ne n
\end{array} \right.\\
\left[ \begin{array}{l}
\left( {{i_1} + {j_1}} \right) - \left( {{i_2} + {j_2}} \right) = n\\
\left( {{i_1} + {j_1}} \right) - \left( {{i_2} + {j_2}} \right) = - n\\
\left( {{i_1} + {j_1}} \right) - \left( {{i_2} + {j_2}} \right) = 0
\end{array} \right.
\end{array} \right.
\end{array} \right.\]$$ $$\[\left[ \begin{array}{l}
\left\{ \begin{array}{l}
{i_1} + {j_1} = n\\
{i_2} + {j_2} = n
\end{array} \right.\\
\left\{ \begin{array}{l}
\left\{ \begin{array}{l}
{i_1} + {j_1} \ne n\\
{i_2} + {j_2} \ne n
\end{array} \right.\\
\left[ \begin{array}{l}
\left( {{i_1} + {j_1}} \right) - \left( {{i_2} + {j_2}} \right) = n\\
\left( {{i_1} + {j_1}} \right) - \left( {{i_2} + {j_2}} \right) = - n\\
\left( {{i_1} + {j_1}} \right) - \left( {{i_2} + {j_2}} \right) = 0
\end{array} \right.
\end{array} \right.
\end{array} \right.\]$$](https://dxdy-04.korotkov.co.uk/f/f/a/a/faa88f8f8ed2cbe60a922bd9225749ca82.png)
И тут возникает разумный вопрос: а что с этим делать? То есть как, используя тот факт что
![$\[{i_1},{i_2},{j_1},{j_2} \in W\]$ $\[{i_1},{i_2},{j_1},{j_2} \in W\]$](https://dxdy-01.korotkov.co.uk/f/c/c/5/cc50e2bef660b7632afee892ab13572282.png)
, подсчитать число решений совокупности? Да и вообще, ничего ли я не упустил в решении, например, целый класс корней, удовлетворяющих условию?