А нельзя ли формулы записать средствами, принятыми на форуме? Прочитайте это:
http://dxdy.ru/viewtopic.php?t=8355 и
http://dxdy.ru/viewtopic.php?t=183. Принцип очень простой:

кодируется a^{n+1},

- a^2,

- \sqrt{3},

- \geqslant,

- \leqslant,
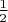
- \frac 12,

- \frac{a+b}{a-b},

- a_3,

- a_{n^2}.
Использовать "звёздочку" в качестве знака умножения в математике не принято, если очень нужен, пишите

или

(\cdot или \times).
Вся формула окружается знаками доллара.
Для исправления служит кнопка "Правка" в правом верхнем углу Вашего сообщения.
И уберите тарабарщину в конце Вашего сообщения.
Если не исправите, придёт модератор и отправит тему в "
Карантин" до исправления.