Планиметрия Задача на решение треугольника

[Mbl_BCE_yMPEM]

Через вершины $A$, $C$ и $A$, $B$ треугольника ${\Delta}ABC$ проведены две окружности $w_1$ и $w_2$ соответственно. Окружности вторично пересекаются в точке $D$, лежащей на стороне $BC$. Из точки $B$ к окружности $w_1$ проведена касательная $BE$. Найти отношение $\frac{AB}{AC}$, если $BE = x$, $BD = y$, $FC =z$, где $F$- точка пересечения $AE$ и $BC$.

Честное слово, даже не знаю с чего начать. Только знаю что ${\angle}ADC={\angle}AEC$ и ${\angle}ADB={\angle}AGB$, где $G$- точка пересечения прямой $BE$ и окружности $w_2$

Еще я понял, что для $\forall$ точки $D\exists!$ пара окружностей $<w_1, w_2>$, которые эту точку пересекают, так как изначально можно взять две (совпадающие) окружности $w_1$ и $w_2$, описанные вокруг треугольника ${\Delta}ABC$, и начать смещать центр каждой из окружности в направлении соответствующей стороны. То есть точка $D$, может быть любой внутренней точкой отрезка $BC$.

[Pphantom]

Тема перемещена из форума «Геометрия» в форум «Карантин»
по следующим причинам:

- неинформативный заголовок;
- отсутствуют собственные содержательные попытки решения задачи.

Исправьте все Ваши ошибки и сообщите об этом в теме Сообщение в карантине исправлено.
Настоятельно рекомендуется ознакомиться с темами Что такое карантин и что нужно делать, чтобы там оказаться и Правила научного форума.

-- 15.11.2018, 00:01 --

Mbl_BCE_yMPEM, замечание за выдающийся оффтопик. Разместить сообщение в теме «ВАЖНО! Прочтите перед написанием сообщения в этот раздел!» - это надо было очень постараться.

[Pphantom]

Тема перемещена из форума «Карантин» в форум «Помогите решить / разобраться (М)»

[Mbl_BCE_yMPEM]

Вот еще, что смог отыскать: по теореме о свойстве касательной и секущей $BE^2=BC{\cdot}BD$, то есть $x^2=BC{\cdot}y$, откуда $BC=\frac{x^2}y$, $DC=\frac{x^2-y^2}y$.

Так же известно, что $AF{\cdot}FE=DF{\cdot}FC=\frac{x^2-y^2-y{\cdot}z}y{\cdot}z$, но тут две неизвестные в уравнении, и как $z$ применить, непонятно.

[DeBill]

Mbl_BCE_yMPEM
Задача некорректна.
1. Сама формулировка сомнительна: первая окружность нигде не задействована более.
2. В задаче - 4 параметра (три задают треугольник, четвертый - точку $D$ на стороне), а заданы лишь три величины. Оно, конечно, в хороших задачах, ответ тем не менее получабелен - но не здесь...
3. Пусть $BE=x=6,BD=y=4,CF=z=3$. Из свойств касательной и секущей находим $BC=9$, и тогда $CD=9-4=5, DF=5-3=2$.
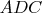
Из подобия треугольников $BDE$ и $BEC$ находим $ED:EC=2:3$. Но $DF:FC$ также равно $2:3$, так что $EF$ - биссектриса угла $DEC$, и потому точка $A$ - середина дуги $DC$, так что $ADC$ - равнобедренный. Потому высота из $A$ приходит в середину $CD$, и если ее длина равна $h$, то $AC^2= h^2+ (2.5)^2, AB^2 = h^2 +(6.5)^2$, и их отношение зависит от $h$ (которое может быть любым). Итого: данных недостаточно.
4. Видимо, в условии что-то пропущено (равенство радиусов? )

[Mbl_BCE_yMPEM]

Спасибо огромное, Вы мне очень помогли. я что то сомневаюсь насчет подобия треугольников $BDE$ и $BEC$. поясните пожалуйста.

[DeBill]

Mbl_BCE_yMPEM в сообщении #1355036 писал(а):

я что то сомневаюсь насчет подобия треугольников

Собственно, свойство касательной и секущей (Вы его выписывали) дает это подобие (пропорциональность сторон плюс общий угол) (но, фактически, оно и выводится из этого подобия: угол между касательной и хордой равен половине дуги. и равен углу, опирающемуся на дугу, стягиваемую хордой. Это дает подобие - по двум углам)

[Mbl_BCE_yMPEM]

Спасибо огромное, от души. А ника Вы точно достойны лучшего!