Квадрат из палочек

[Ktina]

Костя выложил из палочек целочисленной длины квадрат $10\times 10$ (вместе с границей), разбитый на клеточки $1\times 1$. Палочки не пересекаются во внутренних точках. Какое наименьшее число палочек единичной длины могло быть при этом использовано?

(автор задачи - К. Кохась)

[mihaild]

Можно считать что все вертикальные палочки целые имеют длину 10, а горизонтальные, соответственно, 1. Подсчет количества палочек оставим всем желающим в качестве упражнения.

[Ktina]

mihaild
А разве доказывать минимальность разве не нужно?

-- 05.11.2018, 00:40 --

И потом, не все горизонтальные обязаны быть 1, две крайние могут быть тоже 10.

[mihaild]

Да, про крайние забыл. Минимальность очевидна: любое пересечение внутри, где используется две вертикальных палочки, переделывается в использующее одно без увеличения общего числа палочек (склеиваемые вертикальные и при необходимости ломаем горизонтальную)

[wrest]

mihaild
Можно еще оптимальнее, видимо. Для квадрата 4 на 4 у меня получилось 6 единичных палочек (показаны пунктиром).

А по вашему методу нужно 12.

[Sender]

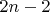
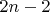
wrest, конструкция, аналогичная вашей, даёт для квадрата со стороной $n$ число единичных палочек $2n-2$. С другой стороны, каждый единичный квадрат, прилегающий к границе, очевидно, должен иметь в качестве стороны хотя бы одну единичную палочку. Всего таких квадратов $4n-4$. Мы можем сгруппировать их попарно, уменьшив вдвое требуемое число единичных палочек. Итак, ответ $2n-2$, что для $n=10$ даёт $18$.

[mihaild]

И правда, заврался я.

[mihaild]

Точнее не заврался, а невнимательно прочитал условия: минимизировали общее число палочек, а не число палочек единичной длины.