Здравствуйте, есть такое задание, система ДУ:

имеет решение:

найдите решение, удовлетворяющее начальным условиям

. В ответе укажите значение

при

.
Решаю по этому примеру (пример 3, адрес с русским названием, наверно поэтому тег url не работает):
http://www.math24.ru/линейные-системы-дифференциальных-уравнений-с-переменными-коэффициентами.html
Ход решения:Первое решение:

Пусть второе линейно-независимое решение выражается векторной функцией:

с начальным условием:

Воспользуемся формулой Лиувилля-Остроградского


 -- Вс ноя 04, 2018 22:52:12 --
-- Вс ноя 04, 2018 22:52:12 --
где
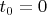

отсюда

рассмотрим второе уравнение исходной системы подставив туда последнее выражение:

И вот тут я остановилась, и так и сяк пыталась решить - не получается, вернее, в итоге получается выражение с интегралом результат которого выражение с гипергеометрическим функциями, чего там, по идее, быть не должно. В итоге я проверила это выражение в
Вольфрамальфа, туда и последнее ДУ подставляла и исходную систему и одно и то же получается выражение в гипергеометрических функциях.
Вопрос:так и должно быть или это я что-то не так делаю, сама склоняюсь больше к первому, потому что решала разными способами и одно и то же получается...