Рассмотрим систему ОДУ:

где

,

и

непрерывна и удовлетворяет локальному условию Липшица. Через

будем обозначать решение задачи Коши такое, что

. Будем предполагать, что решение задачи Коши существует при

.
Множество

назовем
поглощающим для этой системы, если выполнено
(P1) Для всех начальных данных

найдется

такое, что

при всех

.
Назовем множество
 инвариантным
инвариантным, если выполнено
(P2) Если

, то

при всех

.
Известна следующая теорема.
Теорема 1. Если у системы существует компактное поглощающее инвариантное множество

, то существует, по крайней мере одно, ограниченное на всей оси решение.
Доказательство. Для

рассмотрим множества

определяемые как множество начальных данных

таких, что

. Легко видеть, что

в силу
(P2) не пусты. В силу инвариантности (свойства
(P2)) имеем

. Из интегральной непрерывности и замкнутости

следует, что

замкнуты и, следовательно, компактны. Поэтому пересечение

не пусто и содержит хотя бы одну точку

. Очевидно,

есть искомое ограниченное решение.

Для

множество

назовем

-
инвариантным, если выполнено условие
(P2b) Для всех

из того, что

следует, что

для всех

.
Вопрос. Насколько известно следующее обобщение теоремы 1?
Теорема 2. Если у системы существует компактное поглощающее и

-инвариантное множество

, то существует, по крайней мере одно, ограниченное на всей оси решение.
Доказательство. Обобщение получается из того, что последовательность

, определенную в доказательстве теоремы 1, можно разредить, сохранив вложенность. Пусть
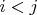
. В силу того, что

, то при

имеем

. Таким образом, можно заполучить подпоследовательность

. Из
(P2b) следует, что

не пусты. Так что найдется точка точка

и

- искомое ограниченное решение.


-инвариантные множества появляются, когда имеется какая-либо оценка на норму решений. Например, для


Легко проверить, что множество

является

-инвариантным и поглощающим.
Разница подходов очень сильно видна на примере линейной системы

с устойчивой матрицей

и ограниченной

. Конечно ограниченные решения тут находятся другими методами по всем известным формулам и в более общих случаях. Но если поставить целью применить тут теоремы 1 или 2, то в первом случае приходится строить специальную функцию Ляпунова, а во втором можно обойтись тупо обычной оценкой по формуле Коши.