При решении неравенства из "Олимпиадного раздела" возникла подозрительно простая идея (а там доказательство далёкое от простого). Идея заключается в следующем: для положительных

1).

,

,

,

2).

,

,

,

Ищется

.
Известно: может быть доказано, что

достигается только при
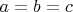
и, не ограничивая общности, можно считать, что

,

,

.
Тогда область определения в пункте

можно представить как

, где


Может быть доказано, что в области

при
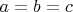
не существует

, т.к. в этой области не определена

при
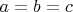
. Тогда

(если существует).
Если идея верна логически, то можно сделать такое обобщение: для положительных


при


Моя попытка обосновать это:
1). Из АМ-ГМ следует, что

достигается только при
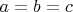
.
2).В области


не достигается, т.к. при
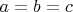
не определена

Вывод:

Если рассуждения не корректны, то прошу объяснить, где именно (желательно привести контрпример), т.к. я ошибки не вижу.