Не для того, чтобы сбить ТС с пути истинного (!), а просто чтобы завершить обзор "неоператорного метода", опишу решение задачи поиска уравнений движения подобным методом ещё в двух примерах.
(Массивное векторное поле)
Главная формула для получения ф.Г. феноменологическим методом уже была написана выше:

Для удобства обозначим присутствующие здесь фурье-образы источников короче - с индексом

вместо аргументов

Обратим внимание: эти аргументы являются компонентами 4-импульса
"на массовой поверхности". Буду их обозначать как

А компоненты произвольного 4-мерного волнового вектора

(у него

- независимая переменная, она не зависит от 3-мерного импульса) буду обозначать как

В левой стороне перейдём к фурье-компонентам, подставив фурье-разложение функции Грина по плоским волнам

и выполнив интегрирование по 4-мерным координатам:


(в последнем равенстве учтено, что в координатном представлении функция источника вещественна:

Тогда исходная формула принимает вид

Это формула в теории скалярного поля. Чтобы обобщить её на многокомпонентные поля, надо считать, что функции источников это "вектор-столбцы" - их компоненты нумеруются каким-то индексом
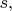
а

- матрица с двумя такими индексами; по индексам ведётся суммирование.
То есть, в правой стороне вместо

будет

В случае массивного векторного поля индекс

должен нумеровать три базисных состояния поляризации частицы (кванта векторного поля). Три компоненты источника

в каждой

-моде определяют амплитуды вероятности рождения частицы (или поглощения частицы, если источник работает как детектор) в этих состояниях поляризации.
Говоря об одной конкретной

-моде, можно вести всё рассмотрение в системе покоя таких частиц. После перехода из произвольной системы отсчёта в систему покоя частицы её 3-импульс

становится равным нулю, так что 4-вектор импульса

будет иметь компоненты

Отсюда видно, что 4-вектор

это единичный вектор, орт временн
ого направления в этой системе отсчёта. В роли единичных векторов трёх базисных направлений поляризации можно выбрать три пространственных орта системы покоя частицы. Такова феноменология модели: считаем, что состояния линейной поляризации векторного поля ведут себя при поворотах как обычные 3-мерные векторы (а не как, например, скаляры или какие-нибудь спиноры). В этой системе отсчёта три

-составляющих источника образуют пространственный вектор

Его проекция на временн
ой орт равна нулю.
В другой системе отсчёта, т.е. после преобразования Лоренца, этот вектор источника останется пространственно-подобным, но у него появится какая-то временн
ая компонента. Значит, в релятивистской теории векторного поля надо описывать источник в каждой моде 4-мерным вектором. Его компоненты

есть

но временн
ая компонента

не является произвольной, так как 4-вектор

должен быть ортогонален единичному 4-вектору

Построить такой 4-вектор легко: числовое значение проекции произвольно заданного 4-вектора

на

то есть свёртку

надо умножить на сам орт

и вычесть получившийся времени-подобный вектор из исходного


В сумму по

входят источники 1 и 2 с одинаковыми

поэтому для них пространственно-подобная гиперплоскость, ортогональная вектору

одна и та же, и, значит, достаточно только в одном источнике выделить указанным способом часть, лежащую в этой гиперплоскости: в свёртку этой части со вторым источником даст вклад только часть второго источника, лежащая в той же гиперплоскости. Таким образом:

Дополнительный множитель

здесь нужен для компенсации минуса в выражении

при

Поскольку выяснилось, что источники у нас 4-векторные, то в лоренц-инвариантной скалярной величине

они должны сворачиваться с матрицей

формата 4х4, представляющей собой 4-тензор второго ранга. Таким образом, на этом этапе наша "главная формула" принимает вид

Чтобы получить отсюда выражение для

осталось придать правой стороне вид 4-кратного интеграла (как в левой стороне) по компонентам произвольного 4-импульса

Для этого можно вспомнить, что множитель

и замена

на

под знаком 3-кратного интеграла по компонентам

возникли из-за полюсов "фейнмановской функции Грина"

в результате интегрирования

Поэтому просто восстановим запись с таким интегралом. Тогда, обозначив

как

и

как

имеем главную формулу в виде

Отсюда получаем искомое выражение фурье-образа функции Грина - "фейнмановского пропагатора массивной векторной частицы":

Тогда классическое поле

, порождаемое 4-векторным источником


есть:

Ну, а дальше можно пробовать действовать на это поле разными комбинациями операторов

(то есть

или

(то есть

Они действуют на экспоненту

, содержащую

и приводят к появлению множителя

или

соответственно.
Проверяется, что оператор

даёт под знаком указанного выше интеграла

для поля

как раз такую комбинацию, которая вместе с комбинацией множителей от

сводится просто к

Так что с этим оператором поле

удовлетворяет уравнению движения

(Безмассовое векторное поле. Уравнения Максвелла.)
Перейти к пределу

в "нашей главной формуле"

препятствует член

Однако его можно просто вычеркнуть ещё до перехода к пределу

если считать, что фурье-образы

любых 4-векторных источников подчинены условию

В координатном представлении это есть "уравнение непрерывности"

то есть

оно интерпретируется как закон сохранение заряда. При этом

интерпретируется как плотность заряда, а

как плотность тока, 4-вектор источника

называют сохраняющимся током.
С этим условием член

вообще не нужно писать, и, значит, перейдя в оставшемся выражении к пределу

можно фурье-образ искомой функции Грина взять просто в виде

(А можно было бы и прибавить к нему выражение

с произвольной скалярной функцией

- такая добавка не даёт вклада в свёртку с сохраняющимся током

Этому произволу в выборе

соответствует свобода выбора "калибровки 4-потенциала"

Из определения классического поля

я в этом примере уберу минус; тогда в итоге получатся общепринятые уравнения (а с минусом у меня получалось, если нигде не ошибся, что наш источник

это

то есть

В принципе-то, наверное, безразлично - считать источником

или

Итак, в безмассовом случае классическое поле

, порождаемое 4-векторным источником

запишем в виде

то есть:

Или, если поднять индекс:

Выбрав

и учитывая, что

видим, что каждая компонента найденного 4-векторного потенциала

удовлетворяет "волновому уравнению с источником"


Аналогично действуя оператором

на

(разумется, с суммированием по

видим, что c учётом

найденное поле удовлетворяет "условию Лоренца":

Взяв от обеих сторон производную

заведомо получим нуль; переставив знаки производных, запишем это так:

Теперь вычитая из обеих сторон этого равенства соответствующие стороны уравнения движения

получаем:

Обозначив

имеем:

Это уравнения Максвелла. Здесь содержится та пара уравнений, в которую входят плотность тока и заряда. Вторая пара уравнений Максвелла содержится в тождестве

оно следует из определения

Всё.
// Только ещё комментарии добавлю - о квантовом физ. смысле той исходной формулы для

с которой здесь начинались примеры. В ней фигурируют лишь классические источники и классическая ф. Г. (правда, "фейнмановская").
1. Почему эта ф. Г. оказывается "пропагатором частицы"?
Вернёмся к формуле для вакуумной амплитуды

(при наличии двух причинно упорядоченных источников):

Перепишем её для случая
слабых источников. Т. е. пусть

и

малы настолько, что в правой стороне можно экспоненты заменить членами разложения низшей степени по

и


Амплитуды вероятности многочастичных процессов в случае слабых источников считаются пренебрежимо малыми. Потому в сумме по конфигурациям частиц остаются только вклад нулевого порядка по источникам, равный единице, и сумма вкладов лишь от одночастичных амплитуд (со всевозможными импульсами частицы, а также значениями индекса поляризации

, если он есть; ниже для краткости не выписываю

Таким образом, в пределе слабых источников:

Левая сторона здесь имеет квантово-механический вид: это амплитуда перехода "вакуум-вакуум" через одночастичное промежуточное состояние, порождаемое источником

с последующим поглощением частицы детектором

Правая сторона содержит чисто классические величины, но теперь при желании можем истолковать её тоже как квантовую амплитуду перехода. Ведь можно детализировать её описание (по крайней мере на словах) так - с амплитудой

первый источник рождает частицу в точке

с амплитудой

второй источник (детектор) поглощает частицу, а

выступает в роли амплитуды распространения частицы от точки

к точке

По 4-координатам

и

ведётся интегрирование. Всё это соответствует квантовым принципам композиции амплитуд вероятности.
2. Ещё один комментарий - о среднем числе частиц

, порождённых классическим источником

за всё время его действия. (Подразумевается наличие квантовых флуктуаций: раз за разом повторяем опыт, и источник то создаст частицы, то не создаст ни одной - тогда вакуум остаётся вакуумом). Исходя из свойств когерентных состояний можно показать (это отдельная учебная задачка), что вероятность перехода "вакуум-вакуум в присутствии источника"

должна иметь вид:

причём среднее число частиц можно представить суммой средних чисел частиц по всем модам:

А амплитуда перехода есть

Подставив сюда

заключаем, что:

Видно, что среднее число частиц квадратично зависит от

Можно уточнить понятие слабого источника так: это источник с

Кроме того, эта формула позволяет проверить, нет ли ошибок в знаке при вычислениях: величина

должна быть неотрицательной.
Для примера посмотрим, что получается в случае источника фотонов (квантов безмассового векторного поля). В этом случае имеем формулу:

Замечаем, что

есть вещественная функция (отметим также, что она чётная).
Следовательно, мнимая часть определяется выражением:

Обе дельта-функции дают равные вклады. Частота теперь в ответ входит только "на массовой поверхности"; чтобы подчеркнуть это, пишем далее

вместо


Заметим, что с учётом

условие сохранения 4-тока принимает на массовой поверхости следующий вид:

так что:

где

- продольная по отношению к

компонента вектора

Можно разложить 3-мерный вектор

на продольную и две поперечные по отношению к

составляющие. Тогда:

Следовательно:

т.е. "временн
ая" и "продольная" компоненты 4-вектора фотонного источника не дают вклада в число созданных источником фотонов. Фотоны, остающиеся после окончания действия источника, - поперечные; число независимых состояний поляризации равно двум:
