Это типа такого:

— шесть штук. Или нельзя одинаковые?
Если можно, то применить ваш любимый арифмост для тройки и легко увидеть, что больше девяти не получится, так как начиная с четвёртого члена последовательность строго возрастает и троек там не будет.
А возможные кандидаты имеют начало
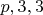
, где
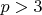
.
Ну вот, например:

Последний, десятый, член неминуемо делится на три