Честно говоря, поначалу мне казалось, что это я опять ошибки делаю, а задание легкое, но с еще десяток попыток вычислить хотябы

довели меня до ручки (до МатКада, тоесть). Я принялся выяснять, как себя ведет данная функция. Честно говоря, я в шоке. Люди добрые, будьте так милостивы, тупо (или умно) вычислите мне
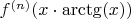
. Достало выкидывать на ветер время.