А разве тут нужна какая-то теорема. Одна подгруппа описывает симметрии сферы с фиксированной точкой, а вторая - симметрии тора. Осталось соединить это в одной фигуре. Выкалываем из сферы полюса и устраняем топологические препятствия, а дальше включаем геометрическое воображение.
Это набор слов, понимания которых вы пока не продемонстрировали. Если вы не можете сформулировать эту фразу в виде теоремы, то я не уверен, что дискуссия будет конструктивной, пока не сможете. К сожалению, за последние 10 лет никакого прогресса в вашем понимании собственных "конструкций" не наблюдается. Грустно на самом деле, некоторые участники форума уже успели по нескольку диссертаций защитить, а вы как не могли натянуть
сову на глобус тор на сферу, так и не можете...
Это вы про базис алгебры Ли, которая порождает одно-параметрическую группу Ли?
Нет. Возьмите какую-нибудь матрицу из

(не кратную единичной). Найдите такую унитарную матрицу

, что
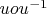
диагональна. Далее, поймите, что если любой элемент

представим в виде

, то с помощью сопряжения матрицей

любой элемент будет представим в виде

.