Наибольшая площадь ортог проекции единичного куба.

[bitcoin]

Здравствуйте! Подскажите, пожалуйста, как найти наибольшую площадь ортог проекции единичного куба.

Я могу дать оценку слету, что эта площадь точно не больше $(2\sqrt{3})^2$ Но вот наибольшую площадь не очень ясно - как искать. Это должен быть, скорее всего - либо прямоугольник, либо шестиугольник. Прямоугольник можно получить, если положить одно ребро куба на плоскость и начать поворачивать этот куб относительно этого ребра. Тогда, скорее всего, площадь проекции будет не более $\sqrt{3}$. Но вот случая с 6-угольником сложнее и может ли быть еще чем-то проекция, помимо прямоуг и шестиугольника? Можете подсказать идею, пожалуйста?

[grizzly]

bitcoin в сообщении #1342651 писал(а):

Я могу дать оценку слету, что эта площадь точно не больше $(2\sqrt{3})^2$

Не очень-то сильная оценка. Попытайтесь доказать, что площадь проекции не может быть больше площади развёртки куба.

[Otta]

bitcoin
На всякий случай. Вы сечение с проекцией не путаете?

[Sender]

grizzly в сообщении #1342656 писал(а):

Попытайтесь доказать, что площадь проекции не может быть больше площади развёртки куба.

И даже больше половины площади развёртки куба, я бы сказал.

[bitcoin]

Otta в сообщении #1342660 писал(а):

bitcoin
На всякий случай. Вы сечение с проекцией не путаете?

Сначала пытался двигать плоскость, на которую делается проекция, были мысли про сечение, но потом увидел контрпример и понял - почему не подходит.

grizzly в сообщении #1342656 писал(а):

Не очень-то сильная оценка. Попытайтесь доказать, что площадь проекции не может быть больше площади развёртки куба.

Согласен, что слабая оценка. А про развертку понял, что площадь ортог проекции каждой грани не может быть больше площади самой грани, отсюда, действительно, следует оценка с разверткой.

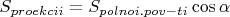
Может ли здесь пригодиться формула, что $S_{proekcii}=S_{polnoi.pov-ti}\cos\alpha$, кстати, эта формула также подтверждает оценку с полной поверхностью. Нам нужно максимизировать косинус? Но он будет равен единице при нулевом угле, получается абсурд

[thething]

Почему абсурд? Это значит, плоскость проекции параллельна чему-то. Думаю, что это "что-то" должно содержать диагональ куба. Доказать пока никак (надо подумать на свежую голову), но ответ видится $\sqrt{3}$.

[grizzly]

Давайте шаг за шагом разбираться с более простыми вещами.

bitcoin в сообщении #1342651 писал(а):

Прямоугольник можно получить, если положить одно ребро куба на плоскость и начать поворачивать этот куб относительно этого ребра. Тогда, скорее всего, площадь проекции будет не более $\sqrt{3}$.

Давайте попробуем посчитать точнее. Ответьте, пожалуйста, последовательно на следующие вопросы:
По какой формуле считается площадь прямоугольника?
Как будут изменяться стороны рассматриваемого прямоугольника при повороте куба относительно зафиксированного Вами ребра?
Для какого положения площадь станет максимальной?

[bitcoin]

grizzly в сообщении #1342708 писал(а):

По какой формуле считается площадь прямоугольника?

Площадь будет считаться по формуле $S=ab$, где $a=1$ - сторона куба, потому $S=b$

grizzly в сообщении #1342708 писал(а):

Как будут изменяться стороны рассматриваемого прямоугольника при повороте куба относительно зафиксированного Вами ребра?

$a=1=\const$, $1\le b\le \sqrt{2}$, то есть $1\le S\le \sqrt{2}$

grizzly в сообщении #1342708 писал(а):

Для какого положения площадь станет максимальной?

Когда диагональ куба будет параллельна той плоскости, на которую будет проецироваться куб, $S_{max}=\sqrt{2}$ для вращения куба вокруг ребра.

[grizzly]

bitcoin
Всё верно. В общем-то единственное, что я могу посоветовать сделать ещё из простого -- посчитать проекцию каждой грани и догадаться, почему теперь можно сделать оценку сверху $3\sqrt{2}/2=3/\sqrt{2}$. Вот что такое $\sqrt{2}$ (полученное Вами выше) с точки зрения проекции граней?
А вот дальше будет сложнее и нужно будет придумать какую-то идею. Но для того, чтобы двинуться дальше, я бы посоветовал сделать рисунок для случая хоть какой-нибудь шестиугольной проекции -- это может сильно помочь.

[DeBill]

bitcoin
Ага, здесь все хорошо.
А про шестиугольник: это - проекция трех граней. Так что шестиугольник этот составлен из трех параллелограммов. Пар-м - он в два раза больше своей половинки. Так что Ваш шестиугольник по площади в два раза больше некоего треугольника...

[Markiyan Hirnyk]

Проекция единичного куба на плоскость является выпуклой оболочкой множества проекциий вершин куба. Не уменьшая общности, одну из вершин единичного куба можно расположить в начале декартовой системы координат. Изложенные соображения сокращают вычисления.

[grizzly]

Markiyan Hirnyk в сообщении #1342730 писал(а):

Изложенные соображения сокращают вычисления.

Вы, должно быть, имеете в виду какие-то сложные вычисления, раз таким образом их можно было бы упростить. Но мы здесь движемся по направлению более простого решения -- идейного, но школьного.

[StaticZero]

(Оффтоп)

grizzly в сообщении #1342734 писал(а):

имеете в виду какие-то сложные вычисления

Ага, в Maple...

[bitcoin]

grizzly в сообщении #1342724 писал(а):

Вот что такое $\sqrt{2}$ (полученное Вами выше) с точки зрения проекции граней?

Это диагональ квадрата. Но я, скорее всего, не так понял вопрос.
А откуда берется $3\sqrt{2}/2=3/\sqrt{2}$. - не знаю. Я лишь понимаю, что если поставить куб на вершину, то каждая точка проекции куба будет получится от минимум 2 точек куба, а значит можно сделать ограничение $3\sqrt{2}$, а вот почему еще в 2 раза меньше - не представляю.

[grizzly]

bitcoin в сообщении #1342766 писал(а):

Но я, скорее всего, не так понял вопрос.

Да, похоже. Представьте себе рисунок, при котором площадь прямоугольной проекции получается $\sqrt 2$. Этот вид сверху симметричен. Каждая половина -- проекция грани. Значит, площадь каждой из двух проекций граней -- $\sqrt 2/2$. Даже если бы Вы смогли добавить третью такую же проекцию, то максимум, чего добились бы -- $3\sqrt 2/2$. Понятно, что третью добавить нельзя, не уменьшая первые две.

Теперь нужен будет рисунок с шестиугольной проекцией. Вы и сами чувствуете, наверное, что пространственного воображения крутить этот кубик в уме Вам не хватает. А для рисунка можете взять в руки любую коробку, повращать по-разному и посмотреть на неё сверху.