Вопросы по математическому моделированию

[dima_1985]

Начал читать книжку Самарского Мат. Моделирование. Некоторые выкладки не понятны. Задача распада вещества
$N_I(t+dt)-N_I(t)=-\alpha N_I(t+\xi dt)$ потом говорят перейдем к дифференциальной форме $\frac{dN_I(t)}{dt}=-\alpha N_I(t)$. Не понятно как сделан этот переход? Я попробовал в ряд разложить $ N_I(t+\xi dt) =N_I(t)+N_I(t)'\xi dt+O(dt^2) $, но из этого ничего не получилось. Спасибо.

[alcoholist]

dima_1985 в сообщении #1342015 писал(а):

Задача распада вещества
$N_I(t+dt)-N_I(t)=-\alpha N_I(t+\xi dt)$

опечатка какая-то: слева бесконечно малая, а справа не пойми что (должно быть $-\alpha N_I(t)dt$: уменьшение $N_I$ пропорционально $N_I$)

[dima_1985]

alcoholist в сообщении #1342016 писал(а):

опечатка какая-то: слева бесконечно малая, а справа не пойми что

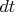
Что-то слишком много опечаток след. рассмотренная задача закон сохранения импульса. Пусть продукты сгорания ракетного топлива покидают расположенные в кормовой части выхлопные сопла со скоростью $ u $. За малый промежуток времени $ dt $ между моментами $t$ и $t+dt$ часть топлива выгорела, и масса ракеты изменилась на величину dm. Изменился также импульс ракеты, однако суммарный импульс "ракета плюс продукты сгорания" остался тем же, что и в момент $t$, т.е.
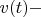
$m(t)v(t) = m(t+dt)v(t+dt)-dm[v(t+\xi dt)-u]$ где $v(t)-$ скорость ракеты, $v(t+\xi dt)-u, 0< \xi < 1 - $ средняя за промежуток $dt$ скорость истекающих из сопел газов (обе скорости относительно Земли). Я правильно понимаю второе слагаемое это изменение массы за интервал времени $dt$ умноженное на изменение скорости? Знак минус так как ракета летит вверх, а газы вниз? Потом пользуются Тейлором $mv = (m+m'dt)(v+v'dt)-dm[v+\xi v' dt - u]$. Если раскрыть скобки и упростить, то $mv'dt + m'dt v'dt - \xi v' dt dm +u dm=0$. Вот тут не очень понятно можно ли сократить $dmdv$ и $-\xi dmdv$? Если да, то получим Д.У. как в учебнике $m\frac{dv}{dt}=-u\frac{dm}{dt}$. Спасибо!

alcoholist в сообщении #1342016 писал(а):

должно быть $-\alpha N_I(t)dt$

Да это я в других источниках нашел.

[alhimikoff]

$dmdv$ это бесконечно малая в квадрате, ей можно пренебречь