Теорема о распределении простых чисел

[math_34]

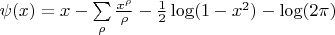
Я хочу построить график пси функции Чебышова, которая есть сумма логарифмов по степеням простых чисел по формуле: $\psi(x)=x-\sum\limits_{\rho}^{}\frac{x^\rho}{\rho}-\frac{1}{2}\log(1-x^2)-\log(2\pi)$ взяв небольшое количество нулей дзета функции. Я хочу просто почувствовать механику процесса. Буду строить график пси в небольшом интервале от 0 до 50.
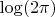
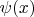
Первый член в правой части это сам x третий член в правой части $\frac{1}{2}\log(1-x^2)$ - это простая функция от х. Четвёртый член в правой части - \log(2\pi)$ - это просто константа. Меня интересует вот это: \sum\limits_{\rho}^{}\frac{x^\rho}{\rho}. Я понимаю, что это сумма по нетривиальным нулям дзета функции, но нуль дзета это комплексное число вида \sigma+it, а значение функции $\psi(x) есть действительное число. Я не понимаю как с этим быть.

[ex-math]

Нули идут комплексно сопряженными парами.
Но ряд по нулям сходится плохо и даже неабсолютно, так что ничего интересного первые нули не дадут.