доброго времени суток. помогите разобраться в следующей задаче:
дан угол

(n - целое), доказать, что можно построить угол в 3 раза меньший тогда и только тогда, когда n не кратно 3.
Итак, нужно понять, когда можно строить
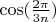
, имея

и действия с квадратичными иррациональностями.
Имеем

минимальный многочлен (косинус тройного угла):

Если этот многочлен неприводим, то степень расширения:
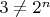
, то есть если он неприводим, то построить его нельзя
Как доказать, что данный многочлен неприводим над первым полем

n

3 ?