В Ленге приводится следующая теорема и доказательство к ней. У меня док-во получилось несколько иным, также я обобщил теорему на произвольное конечное произведение. Хочу проверить, верно ли моё док-во. Ниже формулировка теоремы из Ленга и вложения соответствующих страниц. Затем привожу своё изложение.
Если

- конечная абелева группа, представимая в виде произведения

то

(дуальная к

) изоморфна

Всякая конечная абелева группа изоморфна своей дуальной.
Ленг. Группы. § 11.


Если

- конечная абелева группа, представимая в виде произведения

то

изоморфна

Всякая конечная абелева группа изоморфна своей дуальной.
Построим изоморфизм между

и

Пусть

лежат в

Тогда

Заметим, что показатель

есть нок показателей

поэтому для

порядок
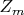
есть нок

и

- подгруппы
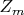
. Группа (циклическая)
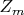
же содержится в прямой сумме (циклических) групп

Определим для

соответствующий эл-т в

положив ля него образом


Определим обратный гомоморфизм, ставя в соответствие для

где

гомоморфизм

что мы можем сделать, поскольку, во-первых,

есть сумма сужений
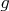
на

, во-вторых,

содержится в прямой сумме групп

, а

- подгруппа в

. Таким образом, мы нашли обратный гомоморфизм, а потому установлен требуемый изоморфизм.
Вторая часть утверждения следует из того, что всякая конечная абелева группа есть прямое произведение циклических групп, для которых данное утверждение легко проверить, с последующим применением первого утверждения теоремы.