Ага!
Вторая попытка...
Пример: пара синих пятиугольников, и паросочетание из 495 синих ребер.
Оценка; Индукция по

: для всех неотрицательных

, если на

вершинах нет синих тр-ков и красных полных подграфов на

вершинах. то синих ребер не менее

База:

,

. Известные школьные задачи: в полном двуцветном графе на 6 вершинах есть либо синий тр-к, либо красный тр-к; в полном двуцветном графе на 9 вершинах есть либо синий тр-к, либо красный полный 4-граф. Поэтому при

утверждение истинно (не бывает таких конфигураций). (Для

: делается шаг индукции как ниже.)

- ШЗ, для

делаем шаг.

- ШЗ

-ШЗ
Шаг:
Если синих ребер не более

, то суммарная синяя полустепень вершин не превышает

. Сумма степеней всех вершин равна

, так что красная полустепень вершин не менее

. В среднем на вершину приходится

, если

(это - в базе). Значит, есть вершина с красной степенью не менее
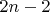
.
Если - в точности
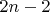
, то из нее выходит ровно одно синее ребро. Удалим его (вместе с концами). Из предположения индукции (

уменьшилось на 1,

сохранилось) получим требуемое.
Если эта вершина - степени

, то удалим ее , и тож будет хорошо (

сохранилось,

увеличилось на 1).
Вааще, можно, навроде, и проще сделать: попросту посмотреть синие степени вершин: если есть степени 0 или 1 - как выше, делается шаг. А если у всех степень не мене 2, то сразу получится что надо - с учетом школьной задачи...
-- 09.09.2018, 07:54 --Упс, есть дырочка: для

шаг по общей методе (как с неравенством, так и попросту) не проходит: один случай (8 вершин, 8 синих ребер, все синие степени вершин равны 2, нет синих тр-ков и красных полных 4-графов) надо рассматривать отдельно. Ну да легко: Это - либо синий восьмиугольник, либо пара синих чет-ков . И тогда есть красный 4-граф -противоречие.
(Да и вообще, можно было сразу уцепиться за наличие синего нечетного цикла длины не менее 5: отсутствие таких сразу дает сине-двудольность; одна из долей - объема не мене половины - что противоречит отсутствию большого красного полного подграфа. Но что то тут у меня не срослось....)