Интегралы, содержащие присоединенные многочлены Лежандра

[van341]

Из дифференциального уравнения для присоединенного многочлена Лежандра [см. например. Е.В. Гобсон. Теория сферических и эллипсоидальных функций] следует, что
$\int\limits_a^b\left[\left(1-x^2\right)^m\frac{d^m}{dx^m}P_n\left(x\right)\right]dx=\displaystyle\left[\frac{-\left(1-x^2\right)^{m+1}\frac{d^{m+1}}{dx^{m+1}}P_n\left(x\right)}{\left(n-m\right)\left(n+m+1\right)}\right]_a^b$. (1)
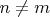
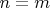
К сожалению соотношение (1) справедливо для $n\ne m$. Для случая $n=m$ используя $n$ раз формулу интегрирования по частям, определение факториала, рекуррентные соотношения для многочленов Лежандра Я получил, что
$\int\limits_a^b\left[\left(1-x^2\right)^n\frac{d^n}{dx^n}P_n\left(x\right)\right]dx=\left[\displaystyle\frac{n!2^n}{2n+1}\sum\limits_{k=0}^n\frac{\left(1-x^2\right)^k}{k!2^k}\frac{\frac{d^k}{dx^k}P_{k+1}\left(x\right)}{2k+1}\right]_a^b$=\left[\displaystyle\frac{n!2^n}{2n+1}\sum\limits_{k=0}^n\frac{P^k_{k}\left(x\right)P^k_{k+1}\left(x\right)}{\left(2k\right)!\left(2k+1\right)}\right]_a^b$. (2)
Полученное выражение (2) содержит сумму, что не совсем удобно. Хотелось бы привести (2) к виду (1).
Подскажите, пожалуйста, встречал ли кто-то нибудь определение или пути решения задачи представления интеграла (2) в виде (1)?

[mihiv]

$\frac {d^n}{dx^n}P_n(x)=(-1)^n\dfrac {(2n)!}{2^nn!}$, поэтому интеграл сводится к: $\int \limits _a^b(1-x^2)^ndx$.