Для чётных

не существует таких чисел. Предлагаю такое доказательство:
Выберем из суммы попарно различных целых чисел наибольшее число

. Докажем, что при

,

больше нашей суммы. Так как

наибольшее целое число, то все числа суммы

чисел представимы в виде

, где

- неотрицательные целые числа. Тогда имеет место такое соотношение
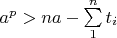
. Соотношение верно, так как при

, а значит правая часть неравенства меньше

При наличии среди


неположительных целых чисел неравенство принимает следующий вид:

.

, значит левая часть меньше

.
Далее докажем, что при

условия задачи также не выполнимы. Чтобы тождество

выполнялось, необходимо, чтобы сумма всех

чисел кроме

обращалась в 0. По условию нужно, чтобы данная сумма, которая равна

являлась степенью всех

чисел, а это возможно только тогда, когда каждое из

чисел являются степенями некоторых чисел

. Так как

- четное число, то

- нечетное, а значит найдется некоторое наибольшее по модулю число

, которое является степенью чисел

или

. Сумма

чисел примет знак этого числа

, так как модуль числа в некоторой степени

больше модуля суммы степеней ниже

этого числа, а значит сумма

чисел при четных

не обращается в 0, и, соответственно, тождество
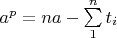
не выполняется при

, а значит и для всех натуральных показателей

при четных

оно не выполняется, ч. т. д.