Я решал почти так же.
Вот красивая картинка к решению (
Wolfram Alpha: y=x^3-2*sqrt(2)*x; -x=y^3-2*sqrt(2)*y):
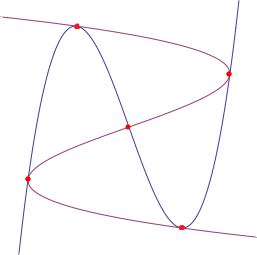
Я только иначе использовал условие касания. Если

— координаты той точки касания, что в первом квадранте, и

, то

, так что получаем систему

Отсюда можно вывести (не находя явно

), что

.