Добрый день.
Задача состоит в том, чтобы исследовать функциональный ряд на сходимость (поточечную и равномерную). Вот этот ряд:

Если обозначить

, то несложно заметить, что

при

. Тогда по признаку Даламбера ряд будет сходится при
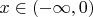
и расходится при

. В 0 тоже получим расходимость.
На множестве
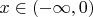
сходимость нашего ряда

равносильна сходимости ряда

при

. Если взять

, то на
![$ t \in (0,r]$ $ t \in (0,r]$](https://dxdy-01.korotkov.co.uk/f/4/0/6/406ddddfc6501ab66ec19cf42b7d580d82.png)
получившийся ряд будет равномерно сходится по признаку Абеля: числитель

можно ограничить 0 и сходящимся к 0 мажорантным рядом

, а оставшаяся часть элемента ряда

образует монотонную стремящуюся к 0 последовательность при фиксированных t. В итоге получили равномерную сходимость на всех отрезках (0, r]

.
Осталось всего-ничего - исследовать на равномерную сходимость на всем интервале (0,1). Есть очень большое подозрение, что в этом случае надо отрицать критерий равномерной сходимости Коши. Но вот что конкретно сказать понятия не имею. Хелп!