Добрый вечер, уважаемые участники форума. Последние несколько дней пытаюсь разобраться в статье Мисюревича про итерации комплексной экспоненты.
https://dropmefiles.com/7aif6 (ссылка ведет на файлообменник, где находится pdf-файл со статьей)
Никак не получается понять начало доказательства леммы 4. А именно, непонятна фраза
Then, by lemma 1,
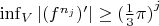
for all

.
У меня получается только доказать, что

. Действительно,

по лемме 1, а

т. к.

не пересекается с

. Но как улучшить эту оценку до

? Буду очень благодарен за любые разъяснения.