корни из единицы и конечнопорожденные Абелевы группы.

[mezon79]

В данный момент занимаюсь одной фундаментальной работой в области теоретической физики. И после описания возникших в теории закономерностей при помощи определенного мат.формализма (комплексного представления), введенного в теорию можно сказать с потолка (основываясь на минимальном наборе логических предпосылок указывающих на целесообразность применения той или иной конкретной алгебры). Возникшие в теории закономерности, сформировали конечные коммутативные группы. Тем самым ответив на вопрос "почему?", в то время кок чистая физика и классическое мат.описание (без привлечения выше-оговоренного мат.формализма), не давали ровным счетом ни какого ответа, на причину возникновения определенных выводов и следствий появившихся в теории.

А сейчас ближе к делу:

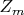
Возникшие в теории группы, оказались группами комплексных корней из единицы соответствующих степеней m, т.е. в экспоненциальной форме: $u_k=e^{\frac{2i\pi}m}^k$, которые изоморфны циклическим группам $Z_m$, порядков m: 20, 12 и 8 соответственно. Причем каждая из данных групп, описывает исключительно свою физическую подсистему, являющуюся частным случаем (представлением), единой физической системы. Точней сказать, различными подходами (точками зрения) в описании одной и той-же физической системы.
Причем группа $Z_8$, описывает минимально возможную подсистему, которую только можно выделить в единой обобщающей системе.

Вопрос:
Так как согласно основной теореме о конечнопорожденных Абелевых группах, группы порядков 20 и 12, возможно представить в виде прямого произведения двух примарных подгрупп, в виде изоморфизмов: $Z_2_0=Z_5\otimes Z_4$; и $Z_1_2=Z_3\otimes Z_4$;
А группа: $Z_8$ не является изоморфной прямому произведению $Z_2\otimes Z_4$.
То следует ли из данного факта, что примененный в описании математический формализм основанный на эллиптических комплексных числах (с мнимой единицей i такой что: $i^2=-1$), не совсем корректен и не в полной мере подходит для описания данных физических подсистем?

Ведь по идее, так как группа $Z_8$ возникает при аналогичном описании одной и той-же физической системы, и отражает один из субъективных подходов в её описании. То и её структура должна быть аналогичной структуре групп: $Z_2_0$ и $Z_1_2$, в которых явно прослеживается наличие подгруппы $Z_4$. И представление группы $Z_8$ в виде изоморфизма прямого произведения двух примарных подгрупп: $Z_8=Z_2\otimes Z_4$, было бы более естественным и логичным?...
Да и степень примарности подгрупп: $Z_5$, $Z_3$ и $Z_2$, по всей видимости не спроста. И может отражать некую скрытую фундаментальную симметрию, лежащую в основе данных подходов рассмотрения единой физической системы?

Возможно ли существование некого расширения используемой алгебры, обобщающего примененный мат.формализм до более общих понятий абстрактной алгебры, и позволяющих описать возникающие в теории группы, в свете единой симметрии их внутренней структуры?