Особые точки и сепаратрисы

[Someone]

Charlz_Klug в сообщении #1327950 писал(а):

А речь шла про решение при конкретных начальных условиях.

Не обязательно. Основным было то, что понятие решения дифференциального уравнения включает интервал, на котором это решение определено: решением дифференциального уравнения на интервале $(a,b)$ называется функция, определённая на этом интервале и удовлетворяющая известным условиям. Рассматривать решение на несвязном множестве в принципе можно, но фактически не интересно, так как решение, определённое на одной части этого множества, невозможно однозначно продолжить на другую часть. Для уравнения $y'=\frac 1x$ решение $y=\ln(-x)$, определённое на интервале $(-\infty,0)$, можно "продолжить" на интервал $(0,+\infty)$ решением $y=\ln x+C$ с любой постоянной $C$. Эти два решения мы никак не можем связать друг с другом, чтобы отдать предпочтение какому нибудь конкретному значению $C$.

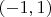
В случае с уравнением $y'=2x$ ситуация была другой. Те два решения, которые я выше рассматривал, не могут быть частями одного решения, так как при продолжении по непрерывности в точку $x=0$ они имеют в этой точке разные значения, так что у нас не получится непрерывной функции на $(-1,1)$. Напротив, требуя непрерывность продолжения, мы можем сделать продолжение однозначным (для дифференциальных уравнений более высокого порядка нужно требовать также непрерывность соответствующего числа производных).

[Charlz_Klug]

Someone, спасибо!