Помогите понять док-во (машины Тьюринга и разрешимость)

[SteelRend]

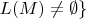
Рассматривается такой язык $(L_{empty})^C = \{x \in (\Sigma_{bool})^\star | x \not= Kod(M)$ для всех МТ $M$, либо $x = Kod(M)$ и $L(M) \not= \emptyset \}$, т.е. дополнение языка $L_{empty} = \{ Kod(M) | L(M) = \emptyset \}$.
Здесь $\Sigma_{bool} = \{0, 1\}$ -- алфавит из двух символов $0$ и $1$, $(\Sigma_{bool})^\star = \{\lambda, 0, 1, 00, 01, ...\}$ -- множество всех слов в алфавите $\Sigma_{bool}$;
$Kod(M)$ -- код машины Тьюринга $M$;
$L(M)$ -- язык, принимаемый МТ $M$.

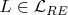
Также, если $L \in \mathcal{L}_{RE}$ (класс рекурсивно перечислимых языков), существует МТ $M$ с принимаемым языком $L = L(M)$, при этом для слова $x \notin L$ МТ $M$ либо работает бесконечно, либо завершает работу в отклоняющем состоянии.


Нужно доказать, что $(L_{empty})^C \in \mathcal{L}_{RE}$ (т.е. существует машина Тьюринга, принимающая этот язык и, возможно, работающая бесконечно на каких-то входах, этому языку не принадлежащих).
Доказательство.
Так как для любой НМТ $M_1$ существует детерминированная МТ $M_2$ такая, что $L(M_1) = L(M_2)$, нам достаточно показать, что существует НМТ $M_1$ с языком $L(M_1) = (L_{empty})^C$. Опишем такую машину, которая работает над входом $x$ следующим образом.

Этап 1. $M_1$ детерминированно проверяет, выполнено ли для некоторой МТ $M$ условие $x = Kod(M)$. Если $x$ не кодирует никакую МТ, то $M_1$ допускает слово $x$.
Этап 2. Если $x = Kod(M)$ для некоторой МТ $M$, то $M_1$ недетерминированно генерирует слово $y \in (\Sigma_{bool})^\star$ и детерминированно моделирует вычисление $M$ над этим словом $y$.
Этап 3. Если $M$ принимает $y$ (т.е. если $L(M) \not= \emptyset$), то $M_1$ допускает свой вход $x = Kod(M)$.
Если $M$ отклоняет $y$, то $M_1$ не принимает $x$ в этом вычислении.
Если вычисление $M$ над $y$ бесконечно, то и $M_1$ не завершает работу над словом $x$ -- и, следовательно, в этом вычислении слово $x = Kod(M)$ не принимается.

Итак, согласно описанию этапа 1, $M_1$ принимает все слова, которые не кодируют машины Тьюринга.
Если $x = Kod(M)$ для некоторой МТ $M$, и при этом $L(M) \not= \emptyset$, то существует слово $y \in L(M)$. Следовательно, существует допускающее вычисление машины $M_1$ над $x = Kod(M)$.
Если же $x \in L_{empty}$, то существует допускающее вычисление машины $M_1$ над словом $x = Kod(M)$ -- и, следовательно $L(M_1) = (L_{empty})^C$.



(взято из книги Ю. Громковича "Теоретическая информатика. Введение в теорию автоматов, теорию вычислимости, теорию сложности, теорию алгоритмов, рандомизацию, теорию связи и криптографию")

=========================================

1. Нет ли в приведенном доказательстве ошибок/возможных опечаток и т.п.?
2. Мне непонятно, что значит

Цитата:

$M_1$ недетерминированно генерирует слово $y \in (\Sigma_{bool})^\star$

Как можно пояснить смысл этого выражения? Что подразумевается под "недетерминированно генерирует слово $y$"?
Работу $M_1$ на Этапе 2 я представляю таким образом. Начиная с пустого слова $y = \lambda$, для текущего слова $y$ МТ $M_1$ имеет три возможных действия:
1) приписать $0$ к слову $y$, т.е. сгенерировать слово $y0$;
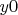
2) приписать $1$ к слову $y$, т.е. сгенерировать слово $y1$;
3) промоделировать работу машины $M$ над словом $y$.
Т.е. у каждого внутреннего узла дерева вычислений машины $M_1$ имеется три потомка, соответствующих этим действиям. В каждом из этих трёх случаев $M_1$ переходит соответственно в состояния $q_{w0}$, $q_{w1}$, $q_w$ (здесь $w$ просто фиксированный символ, не переменное, т.е. речь идёт всего о 3-х состояниях).
Поэтому если $M$ принимает какое-то $y$, то у $M_1$ в дереве вычислений будет присутствовать "моделирующая ветвь", в которой $M$ на входе $y$ завершает работу в допускающем состоянии, и после этого $M_1$ будет принимать свой вход $x = Kod(M)$. При этом если $M$ не имеет конечных вычислений над входом $y$, то $M_1$ также будет работать бесконечно, т.е. она имеет бесконечные вычисления на каких-то входах. Правильно?

[gogoshik]

SteelRend в сообщении #1324421 писал(а):

Мне непонятно, что значит
Цитата:
$M_1$ недетерминированно генерирует слово $y \in (\Sigma_{bool})^\star$
Как можно пояснить смысл этого выражения? Что подразумевается под "недетерминированно генерирует слово $y$"?

Почему Вы не посмотрите здесь: детерминированный алгоритм, здесь НДА-1 и может быть здесь НДА-2.