Можно ли какой-нибудь клетчатый квадрат разрезать по границам
клеток на две фигуры одинакового периметра так, чтобы в одной фигуре клеток было ровно
в 8 раз больше, чем в другой?
Мне удалось это сделать, только квадрат получился уж слишком большой, со стороной 18.
Объясняю патент. Первая фигура содержит все клетки верхней строки квадрата, кроме последней (самой правой), три первые (самые левые) клетки из второй (сверху) строки, а также весь крайний левый столбец. Всё остальное - вторая фигура. Периметры в этом случае будут одинаковыми, а отношение площадей фигур будет
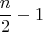
, где

- сторона квадрата. Таким образом, если мы желаем получить отношение, равное 8, нам придётся взять квадрат со стороной 18.
Можно ли выполнить требуемое в задаче на меньшем квадрате?