Найти поток векторного поля

через поверхность тела, ограниченного сферой
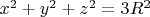
, плоскостью

и однополосным гиперболоидом

.
Решение:
Согласно физическому смыслу поверхностного интеграла, имеем:

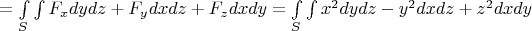
- поток векторного поля
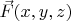
.
Тогда:
На плоскости

и

полученная поверхность проектируется дважды, с обеих сторон, к тому же эта поверхность симметрична относительно этих плоскостей. Поэтому соответствующие интегралы получаются нулевыми:
1)

2)
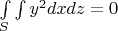
Теперь вычислим интеграл:
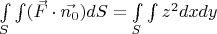
Из уравнения сферы
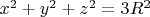
выразим значение

:

Поскольку нормальные векторы полученной поверхности образуют с полуось

острые углы, то переход от поверхностного интеграла второго рода к двойному интегралу осуществляется по формуле:

Следовательно, получим:

. (На это этапе я уже начинаю сомневаться в правильности своего решения.

выражаю из уравнения сферы лишь потому, что полученная фигура своей внешней частью представляет сегмент сферы).
Полученная поверхность состоит из:
1) Сегмента сферы, проекция которого на ось

есть окружность
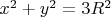
, радиуса

. При этом сегмент сферы пересекается с гиперболоидом по линии

, представляющей собой окружность радиуса
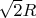
(так как

и

, откуда

,
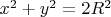
).
2) Сегмента гиперболоида. Он проецируется в кольцо, внутренний радиус которого

, а наружный
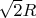
.
Следовательно,

- кольцо, внутренний радиус которого

, а наружный

. (Думаю, что это неверно, так как не учитывается зависимость

от

).
Таким образом, перейдя к полярной системе координат, получим:


Якобиан перехода:

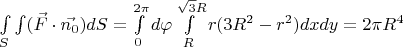
.
Честно, понимаю, что написал неверно. Однако другого решения я придумать не могу.
Как правильно записать интеграл, с помощью которого можно найти поток данного поля через поверхность тела, ограниченного сферой
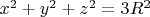
, плоскостью

и однополосным гиперболоидом

?