Текст задачи: Найти уравнение кривой, проходящей через точку

, если для любой точки кривой

произведение ординаты точки пересечения касательной с осью

и квадрата абсциссы точки касания

.
Как я пытался её решить:
Из условий ясно, что

;

- точка касания; уравнение касательной:
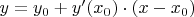
.




Решая методом вариации произвольной постоянной, на первом этапе решая уравнение

получаю:

; на втором этапе решения, решая уравнение

получаю вот этот прекрасный интеграл:

Насколько я знаю, интегралы типа

не берутся.
Правильно ли решена задача? Я склоняюсь к тому, что где-то ошибка.
Пожалуйста помогите решить.
|
i |
Lia: Название темы изменено на содержательное. |