Почему бы не быть такой функции, производная которой равна ln(eˣ+1)?
Такая функция есть, просто её нельзя представить в виде формулы с комбинацией элементарных функций. Но если эта функция где-то будет сильно нужна, математики просто введут для неё своё обозначение, и им можно будет пользоваться наряду с синусами, косинусами, логарифмами и другими элементарными функциями. Можно изучать свойства такой функции, вычислять её значения в точке с нужной точностью, и т.д.
То в результате выходит какая-то муть с функцией erf и тем же выражением с e на хвосте. Эта самая erf, насколько я понимаю, какая-то функция ошибки, которая свидетельствует о том, что интеграл неберущийся. Или нет? Если да, то в каких вообще случаях эта erf появляется и что она вообще значит?
Скорее всего, это вот эта функция:
https://ru.wikipedia.org/wiki/%D0%A4%D1 ... 0%BE%D0%BA - хотя лучше это уточнить в справке для калькулятора. Здесь как раз такая ситуация: математикам стал часто встречаться интеграл от
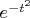
; он существует, но не выражается через элементарные функции, т.е. неберущийся. Вот математики и придумали для него новый символ. Слова "функция ошибок" не свидетельствует, что тут есть какая-то ошибка; просто такое название. И нужно сказать, что далеко не любой неберущийся интеграл будет выражаться через эту самую

; для каких-то других неберущихся интегралов при необходимости придётся давать иные обозначения.