Вычислить поверхностный интеграл первого рода:

, где

- боковая поверхность конуса


.
Решение:
При проецировании фигуры на плоскость

получим:

.
Для решения интеграла имеем:

.
Выразим

:

Тогда:

;

.
Следовательно, получим:

После преобразований:

Перейдем к обобщенной полярной системе координат:


Якобиан перехода:



, так как

, откуда

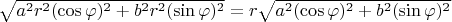
Таким образом, имеем:

Как решать дальше совершенно не понимаю. Полученный интеграл решить не могу.
Вроде бы в вычислениях не запутался, хотя не уверен.
Возможно это задание вообще должно решаться иначе.