Парадокс (теорема) Банаха-Тарского или парадокс удвоения шара — теорема в теории множеств, утверждающая, что трёхмерный шар равносоставлен двум своим копиям.
Два подмножества евклидова пространства называются равносоставленными, если одно можно разбить на конечное число частей, передвинуть их, и составить из них второе. Более точно, два множества

и

являются равносоставленными, если их можно представить как конечное объединение непересекающихся подмножеств
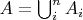
и

так, что для каждого

подмножество

конгруэнтно

.
Если же пользоваться теоремой выбора, то определение звучит так[3]:
<пропущена формула>
Аксиома выбора подразумевает, что существует разбиение поверхности единичной сферы на конечное количество частей, которые преобразованиями трёхмерного Евклидова пространства, не меняющими форму этих составляющих, могут быть собраны в две сферы единичного радиуса.
...
3. M.D. Potter. Set theory and its philosophy: a critical introduction. Oxford University Press, Incorporated, 2004.Как же звучит определение? Какая формула пропущена? Не удалось найти бесплатный доступ к статье [3].