Доказать, что точка пересечения биссектрисы внешнего угла

треугольника

с его описанной окружностью равноудалена от точек
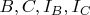
.

Я понимаю, что для того, чтобы доказать равенство

достаточно доказать равенство дуг

или соответствующих вписанных углов опирающихся на эти дуги.
Я пытался пользоваться тем, что центры внепвписанных окружностей лежат на биссекриссе внешних уголов просто углы обозначал разными буквами итп, ничего из этого не помогло пока что. Вижу, что

, как вписанные углы опирающиеся на одну дугу.
Подскажите, пожалуйста, с чего начать, дальше буду думать, развивать мысль, сейчас в тупике.
P.S. Доказательство "внутренней леммы о трезубце" -- понял, понимаю, что здесь должно быть аналогично, но усмотреть аналогию не выходит, потому как здесь нет точки пересечения внутренних биссектрис.