Пример нехаусдорфова пространства

[ikozyrev]

Решаю задачку: привести пример замкнутого подмножества хаусдорфова пространства, фактор по которому не является хаусдорфовым.
Пытался построить такой пример на конечных множествах (троеточие), но ничего не вышло.
Если же взять какое-то неконечное хорошее хаусдорфово пространство (к примеру цилиндр) и взять замкнутое подмножество (например его основание) и сделать фактор по нему то получим топологический конус, который хаусдорфов... мне бы хотябы направление куда копать

-- 18.05.2018, 18:44 --

Хмм, а что если рассмотреть внутренность основания цилиндра как замкнутое множество (в трехмерном пространстве оно и будет замкнутым)? Фактор цилиндра по нему кажется уже нехаусдорфов, да?

[vpb]

ikozyrev
Из евклидова пространства ничего такого не получится. Более точно. Напомним, что пространство $X$ называется
регулярным, если для любой точки $x$ и любого замкнутого множества $M$ с $x\notin M$ существуют
непересекающиеся открытые окрестности $x$ и $M$. Обычно также в определение регулярности включают требование отделимости (т.е. хаусдорфовости). Тогда имеют место утверждения (которые легко доказать самостоятельно):
(а) пространство ${\mathbb R}^n$ регулярно; и конечное отделимое пространство тоже регулярно;
(б) любое подпространство регулярного пространства само регулярно, относительно индуцированной топологии;
(в) фактор регулярного пространства по замкнутому подмножеству отделим.

Таким образом, Вам, по существу, надо построить пример пространства, которое отделимо, но не регулярно.
Не уверен, но, возможно, есть пример такого пространства из счетного множества точек.

(Подумал, вспомнил... Действительно есть такой пример, причем весьма простой. Авось Вы до него сами додумаетесь.)

[ikozyrev]

vpb в сообщении #1313266 писал(а):

ikozyrev
(Подумал, вспомнил... Действительно есть такой пример, причем весьма простой. Авось Вы до него сами додумаетесь.)

Так, ну первое что приходит на ум - взять последовательность $1/n$ но чтобы она оказалась замкнутой тут надо какую-то хитрую топологию вокруг нуля вводить...
Типа выбросить из окресностей нуля все точки $1/n$?

[Someone]

ikozyrev в сообщении #1313309 писал(а):

выбросить из окресностей нуля все точки $1/n$?

Почему бы и нет?

[ikozyrev]

Someone в сообщении #1313313 писал(а):

ikozyrev в сообщении #1313309 писал(а):

выбросить из окресностей нуля все точки $1/n$?

Почему бы и нет?

Ну да вроде все тогда получается, спасибо!

[vpb]

ikozyrev в сообщении #1313309 писал(а):

Так, ну первое что приходит на ум - взять последовательность $1/n$ но чтобы она оказалась замкнутой тут надо какую-то хитрую топологию вокруг нуля вводить...
Типа выбросить из окресностей нуля все точки $1/n$?

Someone в сообщении #1313313 писал(а):

Почему бы и нет?

ikozyrev в сообщении #1313316 писал(а):

Ну да вроде все тогда получается, спасибо!

Не понял, что имеется в виду. Нельзя ли написать подробнее ? А то как бы ТС не впал в самообман (ну, или у меня в понятиях кое-что подправить...).

[ikozyrev]

Цитата:

Не понял, что имеется в виду. Нельзя ли написать подробнее ? А то как бы ТС не впал в самообман (ну, или у меня в понятиях кое-что подправить...).

Нашел в Колмогорове (функан стр. 104) (я ведь помнил эту тему!):

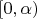
Примером хаусдорфова пространства, не являющегося регулярным, может служить отрезок $[0,1]$, в котором окрестности всех точек, кроме точки 0, определяются обычным способом, а окрестностями нуля считаются всемозможные полуинтервалы $[0,\alpha)$, из которых выкинуты точки вида $1/n$. Это - хаусдорфово пространство, но в нем точка 0 и не содержащее ее замкнутое множество $\{1/n\}$ не отделимы друг от друга.


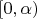
И вот тут я призадумался. Я уверен что Колмогоров конечно прав, но если взять объединение любого открытого множества $[0,\alpha)$ и окрестностей точек $1/n$, то получится открытое множество, верно? Тогда оно будет окрестностью точки 0. И будет содержать хотя бы одну точку из $\{1/n\}$. А значит 0 - будет предельной для $\{1/n\}$. А значит $\{1/n\}$ - не замкнуто. Где я ошибаюсь?

[Mikhail_K]

ikozyrev в сообщении #1313377 писал(а):

Тогда оно будет окрестностью точки 0. И будет содержать хотя бы одну точку из $\{1/n\}$. А значит 0 - будет предельной для $\{1/n\}$.

Вот в этом "а значит" ошибка. Вспомните определение предельной точки, какой там квантор. Если какая-то окрестность точки $0$ содержит точки из какого-то множества, отсюда ещё не следует, что точка $0$ для него предельная.

Этак можно додуматься и до того, что точка $0$ является предельной для множества $[1,\,2]$ в стандартной топологии. А что, окрестность нуля $(-3,\,3)$ вполне содержит точки из $[1,\,2]$.

[ikozyrev]

Mikhail_K в сообщении #1313379 писал(а):

ikozyrev в сообщении #1313377 писал(а):

Тогда оно будет окрестностью точки 0. И будет содержать хотя бы одну точку из $\{1/n\}$. А значит 0 - будет предельной для $\{1/n\}$.

Вот в этом "а значит" ошибка. Вспомните определение предельной точки, какой там квантор. Если какая-то окрестность точки $0$ содержит точки из какого-то множества, отсюда ещё не следует, что точка $0$ для него предельная.

Этак можно додуматься и до того, что точка $0$ является предельной для множества $[1,\,2]$ в стандартной топологии. А что, окрестность нуля $(-3,\,3)$ вполне содержит точки из $[1,\,2]$.

Да, пока писал уже сам понял...

[vpb]

ikozyrev
Спасибо за объяснение. А я, напротив, ошибся, в том смысле, что отделимое не регулярное пространство счетной мощности возможно и существует, но тот "пример" такого пространства, который был у меня в голове, ошибочен.

[Someone]

vpb в сообщении #1313417 писал(а):

отделимое не регулярное пространство счетной мощности возможно и существует, но тот "пример" такого пространства, который был у меня в голове, ошибочен

Я не знаю, что у Вас в голове, но если мы в указанном выше примере из учебника оставим только рациональные точки, то получится как раз требуемое счётное пространство.

[vpb]

Someone в сообщении #1313423 писал(а):

Я не знаю, что у Вас в голове, но если мы в указанном выше примере из учебника оставим только рациональные точки, то получится как раз требуемое счётное пространство.

Понятно.